本文简要介绍 python 语言中 scipy.special.kvp 的用法。
用法:
scipy.special.kvp(v, z, n=1)#计算 real-order 修正贝塞尔函数 Kv(z) 的导数
Kv(z) 是第二类修正贝塞尔函数。导数是相对于 z 计算的。
- v: 类似浮点数的数组
贝塞尔函数的阶
- z: 复杂的数组
评估导数的参数
- n: 整数,默认 1
导数的顺序。对于 0,返回贝塞尔函数
kv本身。
- out: ndarray
结果
参数 ::
返回 ::
注意:
使用关系 DLFM 10.29.5 [2] 计算导数。
参考:
[1]张善杰和金建明。 “特殊函数的计算”,John Wiley and Sons,1996 年,第 6 章。https://people.sc.fsu.edu/~jburkardt/f77_src/special_functions/special_functions.html
[2]NIST 数学函数数字 Library 。 https://dlmf.nist.gov/10.29.E5
例子:
计算第二类 0 阶修正贝塞尔函数及其在 1 处的前两个导数。
>>> from scipy.special import kvp >>> kvp(0, 1, 0), kvp(0, 1, 1), kvp(0, 1, 2) (0.42102443824070834, -0.6019072301972346, 1.0229316684379428)通过提供 v 的数组,计算 1 处多个阶数的第二类修正贝塞尔函数的一阶导数。
>>> kvp([0, 1, 2], 1, 1) array([-0.60190723, -1.02293167, -3.85158503])通过提供 z 的数组,计算第二类 0 阶修正贝塞尔函数在多个点的一阶导数。
>>> import numpy as np >>> points = np.array([0.5, 1.5, 3.]) >>> kvp(0, points, 1) array([-1.65644112, -0.2773878 , -0.04015643])绘制第二类修正贝塞尔函数及其前三个导数。
>>> import matplotlib.pyplot as plt >>> x = np.linspace(0, 5, 1000) >>> fig, ax = plt.subplots() >>> ax.plot(x, kvp(1, x, 0), label=r"$K_1$") >>> ax.plot(x, kvp(1, x, 1), label=r"$K_1'$") >>> ax.plot(x, kvp(1, x, 2), label=r"$K_1''$") >>> ax.plot(x, kvp(1, x, 3), label=r"$K_1'''$") >>> ax.set_ylim(-2.5, 2.5) >>> plt.legend() >>> plt.show()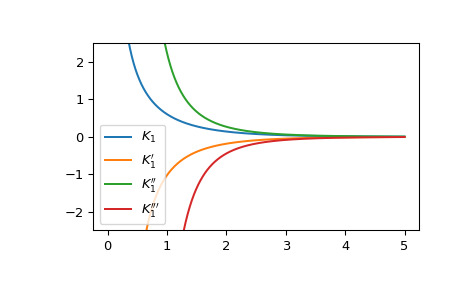
相关用法
- Python SciPy special.kve用法及代码示例
- Python SciPy special.kv用法及代码示例
- Python SciPy special.ker用法及代码示例
- Python SciPy special.k0e用法及代码示例
- Python SciPy special.kolmogorov用法及代码示例
- Python SciPy special.k1e用法及代码示例
- Python SciPy special.kn用法及代码示例
- Python SciPy special.k1用法及代码示例
- Python SciPy special.k0用法及代码示例
- Python SciPy special.kei用法及代码示例
- Python SciPy special.kolmogi用法及代码示例
- Python SciPy special.exp1用法及代码示例
- Python SciPy special.expn用法及代码示例
- Python SciPy special.ncfdtri用法及代码示例
- Python SciPy special.gamma用法及代码示例
- Python SciPy special.y1用法及代码示例
- Python SciPy special.y0用法及代码示例
- Python SciPy special.ellip_harm_2用法及代码示例
- Python SciPy special.i1e用法及代码示例
- Python SciPy special.smirnovi用法及代码示例
- Python SciPy special.ynp_zeros用法及代码示例
- Python SciPy special.j1用法及代码示例
- Python SciPy special.logsumexp用法及代码示例
- Python SciPy special.expit用法及代码示例
- Python SciPy special.polygamma用法及代码示例
注:本文由纯净天空筛选整理自scipy.org大神的英文原创作品 scipy.special.kvp。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
