Python numpy Generator.standard_t用法及代码示例

本文简要介绍 python 语言中 numpy.random.Generator.standard_t 的用法。

用法:

random.Generator.standard_t(df, size=None)

从具有 df 自由度的标准学生 t 分布中抽取样本。

双曲分布的一个特例。作为df变大，结果类似于标准正态分布的结果(numpy.random.Generator.standard_normal)。

参数：

df： 浮点数或类似数组的浮点数

自由度，必须 > 0。

size： int 或整数元组，可选

输出形状。例如，如果给定的形状是 (m, n, k) ，则绘制 m * n * k 样本。如果 size 为 None(默认)，如果 df 是标量，则返回单个值。否则，将抽取np.array(df).size 样本。

返回：

out： ndarray 或标量

从参数化的标准学生 t 分布中抽取样本。

注意：

t 分布的概率密度函数为

\[P(x, df) = \frac{\Gamma(\frac{df+1}{2})}{\sqrt{\pi df} \Gamma(\frac{df}{2})}\Bigl( 1+\frac{x^2}{df} \Bigr)^{-(df+1)/2}\]

t 检验基于数据来自正态分布的假设。 t 检验提供了一种方法来测试样本均值(即根据数据计算的均值)是否是对真实均值的良好估计。

1908 年，William Gosset 在都柏林的吉尼斯啤酒厂工作时首次发表了 t 分布的推导。由于专有问题，他不得不以化名发表，所以他使用了学生这个名字。

参考：

1：

Dalgaard, Peter，“R 的介绍性统计”，Springer，2002 年。

2：

维基百科，“学生的 t 分布”https://en.wikipedia.org/wiki/Student’s_t-distribution

例子：

从 Dalgaard 第 83 页 [1] 中，假设 11 名女性的每日能量摄入量(以千焦耳 (kJ) 为单位)为：

>>> intake = np.array([5260., 5470, 5640, 6180, 6390, 6515, 6805, 7515, \
...                    7515, 8230, 8770])

他们的能量摄入是否系统地偏离了 7725 kJ 的推荐值？我们的零假设将是不存在偏差，而替代假设将是存在可能是正面或负面的影响，因此使我们的测试成为 2 尾。

因为我们正在估计平均值并且我们的样本中有 N=11 个值，所以我们有 N-1=10 个自由度。我们将显著性水平设置为 95%，并使用我们摄入量的经验平均值和经验标准差计算 t 统计量。我们使用 1 的 ddof 将经验标准偏差的计算基于方差的无偏估计(注意：由于平方根的凹性质，最终估计不是无偏的)。

>>> np.mean(intake)
6753.636363636364
>>> intake.std(ddof=1)
1142.1232221373727
>>> t = (np.mean(intake)-7725)/(intake.std(ddof=1)/np.sqrt(len(intake)))
>>> t
-2.8207540608310198

我们从具有足够自由度的学生 t 分布中抽取 1000000 个样本。

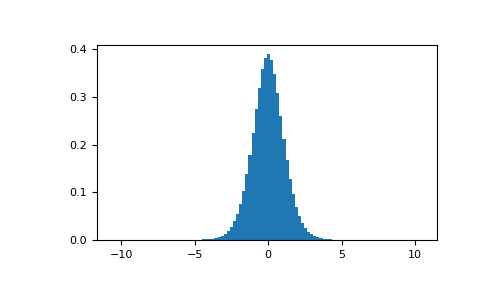
>>> import matplotlib.pyplot as plt
>>> s = np.random.default_rng().standard_t(10, size=1000000)
>>> h = plt.hist(s, bins=100, density=True)

我们的 t 统计量是否落在分布两端的两个关键区域之一？

>>> np.sum(np.abs(t) < np.abs(s)) / float(len(s))
0.018318  #random < 0.05, statistic is in critical region

这个 2 尾检验的概率值约为 1.83%，低于 5% 的预先确定的显著性阈值。

因此，在零假设为真的条件下观察到像我们的摄入一样极端的值的概率太低，我们拒绝没有偏差的零假设。