本文简要介绍 python 语言中 numpy.random.Generator.pareto 的用法。
用法:
random.Generator.pareto(a, size=None)从具有指定形状的 Pareto II 或 Lomax 分布中抽取样本。
Lomax 或 Pareto II 分布是移动的 Pareto 分布。经典的帕累托分布可以通过加 1 并乘以尺度参数
m(见注释)从 Lomax 分布中获得。 Lomax 分布的最小值为零,而对于经典 Pareto 分布,它是mu,其中标准 Pareto 分布的位置为mu = 1。 Lomax 也可以被认为是广义帕累托分布(在 SciPy 中可用)的简化版本,比例设置为 1,位置设置为零。帕累托分布必须大于零,并且在上面是无界的。它也被称为“80-20 法则”。在此分布中,80% 的权重位于范围的最低 20% 范围内,而其他 20% 的权重填充范围的剩余 80%。
- a: 浮点数或类似数组的浮点数
分布的形状。必须是正的。
- size: int 或整数元组,可选
输出形状。例如,如果给定的形状是
(m, n, k),则绘制m * n * k样本。如果 size 为None(默认),如果a是标量,则返回单个值。否则,将抽取np.array(a).size样本。
- out: ndarray 或标量
从参数化的帕累托分布中抽取样本。
参数:
返回:
注意:
帕累托分布的概率密度是
其中 是形状, 是比例。
帕累托分布以意大利经济学家维尔弗雷多·帕累托的名字命名,是一种幂律概率分布,可用于许多现实世界的问题。在经济学领域之外,它通常被称为布拉德福德分布。帕累托发展了分配来说明经济中的财富分配。它还用于保险、网页访问统计、油田规模和许多其他问题,包括 Sourceforge 中项目的下载频率 [1]。它是所谓的 “fat-tailed” 发行版之一。
参考:
Francis Hunt 和 Paul Johnson,关于 Sourceforge 项目的帕累托分布。
帕累托五世 (1896)。政治经济学课程。洛桑。
Reiss, R.D., Thomas, M.(2001),极值的统计分析,Birkhauser Verlag,巴塞尔,第 23-30 页。
维基百科,“Pareto distribution”,https://en.wikipedia.org/wiki/Pareto_distribution
1:
2:
3:
4:
例子:
从分布中抽取样本:
>>> a, m = 3., 2. # shape and mode >>> s = (np.random.default_rng().pareto(a, 1000) + 1) * m显示样本的直方图以及概率密度函数:
>>> import matplotlib.pyplot as plt >>> count, bins, _ = plt.hist(s, 100, density=True) >>> fit = a*m**a / bins**(a+1) >>> plt.plot(bins, max(count)*fit/max(fit), linewidth=2, color='r') >>> plt.show()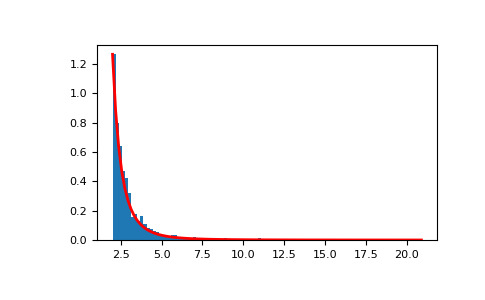
相关用法
- Python numpy Generator.poisson用法及代码示例
- Python numpy Generator.power用法及代码示例
- Python numpy Generator.permutation用法及代码示例
- Python numpy Generator.permuted用法及代码示例
- Python numpy Generator.multivariate_normal用法及代码示例
- Python numpy Generator.standard_normal用法及代码示例
- Python numpy Generator.bytes用法及代码示例
- Python numpy Generator.shuffle用法及代码示例
- Python numpy Generator.choice用法及代码示例
- Python numpy Generator.random用法及代码示例
- Python numpy Generator.logseries用法及代码示例
- Python numpy Generator.uniform用法及代码示例
- Python numpy Generator.standard_t用法及代码示例
- Python numpy Generator.standard_cauchy用法及代码示例
- Python numpy Generator.normal用法及代码示例
- Python numpy Generator.geometric用法及代码示例
- Python numpy Generator.laplace用法及代码示例
- Python numpy Generator.vonmises用法及代码示例
- Python numpy Generator.noncentral_f用法及代码示例
- Python numpy Generator.gamma用法及代码示例
- Python numpy Generator.multivariate_hypergeometric用法及代码示例
- Python numpy Generator.weibull用法及代码示例
- Python numpy Generator.gumbel用法及代码示例
- Python numpy Generator.noncentral_chisquare用法及代码示例
- Python numpy Generator.negative_binomial用法及代码示例
注:本文由纯净天空筛选整理自numpy.org大神的英文原创作品 numpy.random.Generator.pareto。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
