Python SciPy stats.shapiro用法及代码示例

本文简要介绍 python 语言中 scipy.stats.shapiro 的用法。

用法:

scipy.stats.shapiro(x)#

执行Shapiro-Wilk 正态性检验。

Shapiro-Wilk 检验检验数据来自正态分布的原假设。

参数 ：：

x： array_like

样本数据数组。

返回 ：：

statistic： 浮点数

检验统计量。

p-value： 浮点数

假设检验的 p 值。

注意：

所使用的算法在[4]中进行了说明，但所说明的审查参数并未实现。对于 N > 5000，W 检验统计量准确，但 p 值可能不准确。

参考：

[1]

https://www.itl.nist.gov/div898/handbook/prc/section2/prc213.htm DOI:10.18434/M32189

[2] (1,2)

Shapiro, S. S. & Wilk, M.B，“正态性方差检验分析(完整样本)”，Biometrika，1965 年，第 1 卷。 52，第 591-611 页，DOI:10.2307/2333709

[3]

Razali, N. M. 和 Wah, Y. B.，“Shapiro-Wilk、Kolmogorov-Smirnov、Lilliefors 和 Anderson-Darling 测试的功效比较”，《统计建模与分析杂志》，2011 年，第 1 卷。 2，第 21-33 页。

[4]

Royston P.，“备注 AS R94：对算法 AS 181 的备注：正态性的 W-test”，1995 年，应用统计学，卷。 44、DOI:10.2307/2986146

[5]

Phipson B. 和 Smyth, G. K.，“排列 P 值不应该为零：随机绘制排列时计算精确的 P 值”，遗传学和分子生物学中的统计应用，2010 年，第 9 卷，DOI:10.2202/1544-6115.1585

[6]

Panagiotakos, D. B.，“p 值在生物医学研究中的值”，开放心血管医学杂志，2008 年，第 2 卷，第 97-99 页，DOI:10.2174/1874192400802010097

例子：

假设我们希望从测量中推断医学研究中成年男性的体重是否不服从正态分布 [2]。重量(磅)记录在下面的数组x中。

>>> import numpy as np
>>> x = np.array([148, 154, 158, 160, 161, 162, 166, 170, 182, 195, 236])

[1] 和 [2] 的正态性检验首先根据观测值与正态分布的预期阶统计量之间的关系计算统计量。

>>> from scipy import stats
>>> res = stats.shapiro(x)
>>> res.statistic
0.7888147830963135

对于从正态分布中抽取的样本，此统计量的值往往较高(接近 1)。

通过将统计量的观察值与零分布进行比较来执行检验：零分布是在权重从正态分布中得出的零假设下形成的统计值的分布。对于这种正态性检验，零分布不容易准确计算，因此通常采用蒙特卡罗方法来近似，即从正态分布中抽取许多与x大小相同的样本并计算统计量的值对于每个。

>>> def statistic(x):
...     # Get only the `shapiro` statistic; ignore its p-value
...     return stats.shapiro(x).statistic
>>> ref = stats.monte_carlo_test(x, stats.norm.rvs, statistic,
...                              alternative='less')
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(figsize=(8, 5))
>>> bins = np.linspace(0.65, 1, 50)
>>> def plot(ax):  # we'll re-use this
...     ax.hist(ref.null_distribution, density=True, bins=bins)
...     ax.set_title("Shapiro-Wilk Test Null Distribution \n"
...                  "(Monte Carlo Approximation, 11 Observations)")
...     ax.set_xlabel("statistic")
...     ax.set_ylabel("probability density")
>>> plot(ax)
>>> plt.show()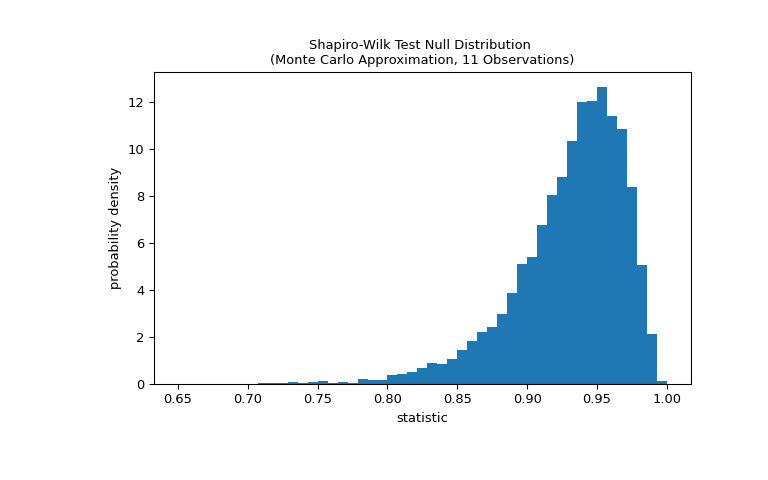

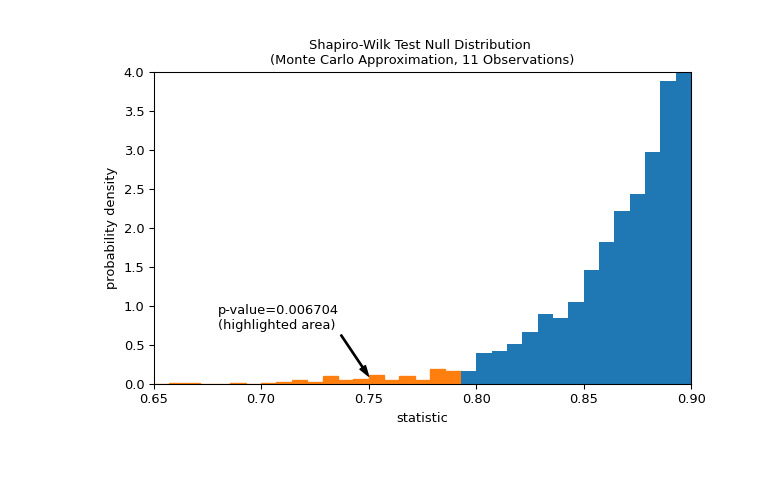
比较通过 p 值进行量化：零分布中小于或等于统计观测值的值的比例。

>>> fig, ax = plt.subplots(figsize=(8, 5))
>>> plot(ax)
>>> annotation = (f'p-value={res.pvalue:.6f}\n(highlighted area)')
>>> props = dict(facecolor='black', width=1, headwidth=5, headlength=8)
>>> _ = ax.annotate(annotation, (0.75, 0.1), (0.68, 0.7), arrowprops=props)
>>> i_extreme = np.where(bins <= res.statistic)[0]
>>> for i in i_extreme:
...     ax.patches[i].set_color('C1')
>>> plt.xlim(0.65, 0.9)
>>> plt.ylim(0, 4)
>>> plt.show
>>> res.pvalue
0.006703833118081093

如果 p 值为 “small” - 也就是说，如果从正态分布总体中采样数据产生统计数据的极值的概率较低 - 这可以作为反对零假设的证据另一种选择：权重不是从正态分布中得出的。注意：

• 反之则不成立；也就是说，检验不用于为原假设提供证据。

• 将被视为 “small” 的值的阈值是在分析数据之前应做出的选择 [5]，同时考虑误报(错误地拒绝原假设)和漏报(未能拒绝假设)的风险。错误的原假设)。