本文简要介绍 python 语言中 scipy.stats.levy_stable 的用法。
用法:
scipy.stats.levy_stable = <scipy.stats._levy_stable.levy_stable_gen object>#Levy-stable 连续随机变量。
作为
rv_continuous类的实例,levy_stable对象从它继承了一组通用方法(完整列表见下文),并用特定于此特定发行版的详细信息来完成它们。注意:
levy_stable的分布具有特征函数:其中支持两种不同的参数化。第一个 :
第二个 :
levy_stable的概率密度函数为:其中 。这个积分没有已知的封闭形式。
levy_stable概括了几种分布。如果可能的话,应该使用它们。具体来说,当形状参数采用下表中的值时,应使用相应的等效分布。alphabeta相等的
1/2
-1
1/2
1
1
0
2
any
norm(与scale=sqrt(2))默认情况下,对 pdf 的评估使用 Nolan 的分段积分方法和 Zolotarev 参数化。还可以选择使用特征函数的标准参数化的直接数值积分或通过特征函数的 FFT 进行评估。
可以通过将类变量
levy_stable.pdf_default_method设置为 Nolan 方法的 ‘piecewise’、直接数值积分的 ‘dni’ 或基于 FFT 的方法的“fft-simpson”之一来更改默认方法。为了向后兼容,方法‘best’和‘zolotarev’相当于‘piecewise’,方法‘quadrature’相当于‘dni’。可以通过将类变量
levy_stable.parameterization设置为“S0”或“S1”来更改参数化。默认值为“S1”。为了提高分段和直接数值积分的性能,可以指定
levy_stable.quad_eps(默认为 1.2e-14)。这既用作直接数值积分的绝对和相对正交公差,也用作分段方法的相对正交公差。还可以指定levy_stable.piecewise_x_tol_near_zeta(默认为 0.005)来表示 x 在被认为与 x [NO] 相同之前与 zeta 的接近程度。确切的检查是abs(x0 - zeta) < piecewise_x_tol_near_zeta*alpha**(1/alpha)。还可以指定levy_stable.piecewise_alpha_tol_near_one(默认为 0.005)来表示 alpha 在被认为等于 1 之前与 1 的接近程度。为了提高 FFT 计算的准确性,可以指定
levy_stable.pdf_fft_grid_spacing(默认为 0.001)和pdf_fft_n_points_two_power(默认为 None,这意味着计算的值足以覆盖输入范围)。通过设置
pdf_fft_interpolation_degree(默认为 3)为样条顺序和pdf_fft_interpolation_level来确定在逼近特征函数时在 Newton-Cotes 公式中使用的点数,可以进一步控制 FFT 计算(被认为是实验性的)。默认情况下,cdf 的评估使用 Nolan 的分段积分方法和 Zolatarev 参数化。还可以选择通过积分通过 FFT 方法计算的 pdf 的插值样条进行评估。影响 FFT 计算的设置与 pdf 计算相同。可以通过将
levy_stable.cdf_default_method设置为 ‘piecewise’ 或“fft-simpson”来更改默认 cdf 方法。对于 cdf 计算,Zolatarev 方法的准确性更高,因此默认情况下禁用 FFT。拟合估计使用[MC]中的分位数估计方法。拟合方法中参数的 MLE 估计最初使用此分位数估计。请注意,如果使用 FFT 进行 pdf 计算,MLE 并不总是收敛;如果 alpha <= 1,FFT 方法不能给出好的近似值,就会出现这种情况。
如果未设置有效的默认方法,则属性
levy_stable.pdf_fft_min_points_threshold的任何非缺失值都会将levy_stable.pdf_default_method设置为“fft-simpson”。警告
对于 pdf 计算,FFT 计算被认为是实验性的。
对于 cdf 计算,FFT 计算被认为是实验性的。改用 Zolatarev 的方法(默认)。
上面的概率密度以“standardized” 形式定义。要移动和/或缩放分布,请使用
loc和scale参数。通常,levy_stable.pdf(x, alpha, beta, loc, scale)与levy_stable.pdf(y, alpha, beta) / scale和y = (x - loc) / scale完全相同,除非在S1参数化中alpha == 1。在这种情况下,levy_stable.pdf(x, alpha, beta, loc, scale)等同于levy_stable.pdf(y, alpha, beta) / scale和y = (x - loc - 2 * beta * scale * np.log(scale) / np.pi) / scale。更多信息请参见[NO2]定义1.8。请注意,移动分布的位置不会使其成为“noncentral”分布。参考:
[MC]McCulloch, J., 1986。稳定分布参数的简单一致估计。统计通信 - 模拟和计算 15, 11091136。
[WZ]Wang、Li 和 Zhang,Ji-Hong,2008 年。基于 Simpson 规则的 FFT 方法计算稳定分布的密度。
[NO]Nolan, J., 1997。稳定密度和分布函数的数值计算。
[二氧化氮]Nolan, J.,2018。稳定分布:重尾数据模型。
[HO]Hopcraft, K. I., Jakeman, E., Tanner, R. M. J., 1999。具有波动步数和多尺度行为的 Lévy 随机游走。
例子:
>>> import numpy as np >>> from scipy.stats import levy_stable >>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots(1, 1)计算前四个时刻:
>>> alpha, beta = 1.8, -0.5 >>> mean, var, skew, kurt = levy_stable.stats(alpha, beta, moments='mvsk')显示概率密度函数(
pdf):>>> x = np.linspace(levy_stable.ppf(0.01, alpha, beta), ... levy_stable.ppf(0.99, alpha, beta), 100) >>> ax.plot(x, levy_stable.pdf(x, alpha, beta), ... 'r-', lw=5, alpha=0.6, label='levy_stable pdf')或者,可以调用分布对象(作为函数)来固定形状、位置和比例参数。这将返回一个 “frozen” RV 对象,其中包含固定的给定参数。
冻结分布并显示冻结的
pdf:>>> rv = levy_stable(alpha, beta) >>> ax.plot(x, rv.pdf(x), 'k-', lw=2, label='frozen pdf')检查
cdf和ppf的准确性:>>> vals = levy_stable.ppf([0.001, 0.5, 0.999], alpha, beta) >>> np.allclose([0.001, 0.5, 0.999], levy_stable.cdf(vals, alpha, beta)) True生成随机数:
>>> r = levy_stable.rvs(alpha, beta, size=1000)并比较直方图:
>>> ax.hist(r, density=True, bins='auto', histtype='stepfilled', alpha=0.2) >>> ax.set_xlim([x[0], x[-1]]) >>> ax.legend(loc='best', frameon=False) >>> plt.show()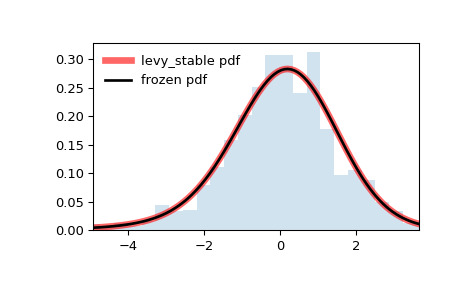
相关用法
- Python SciPy stats.levy_l用法及代码示例
- Python SciPy stats.levy用法及代码示例
- Python SciPy stats.levene用法及代码示例
- Python SciPy stats.lognorm用法及代码示例
- Python SciPy stats.logrank用法及代码示例
- Python SciPy stats.loglaplace用法及代码示例
- Python SciPy stats.laplace用法及代码示例
- Python SciPy stats.linregress用法及代码示例
- Python SciPy stats.loguniform用法及代码示例
- Python SciPy stats.logistic用法及代码示例
- Python SciPy stats.logser用法及代码示例
- Python SciPy stats.loggamma用法及代码示例
- Python SciPy stats.lomax用法及代码示例
- Python SciPy stats.laplace_asymmetric用法及代码示例
- Python SciPy stats.anderson用法及代码示例
- Python SciPy stats.iqr用法及代码示例
- Python SciPy stats.genpareto用法及代码示例
- Python SciPy stats.skewnorm用法及代码示例
- Python SciPy stats.cosine用法及代码示例
- Python SciPy stats.norminvgauss用法及代码示例
- Python SciPy stats.directional_stats用法及代码示例
- Python SciPy stats.invwishart用法及代码示例
- Python SciPy stats.bartlett用法及代码示例
- Python SciPy stats.page_trend_test用法及代码示例
- Python SciPy stats.itemfreq用法及代码示例
注:本文由纯净天空筛选整理自scipy.org大神的英文原创作品 scipy.stats.levy_stable。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
