Python SciPy stats.logrank用法及代码示例

本文简要介绍 python 语言中 scipy.stats.logrank 的用法。

用法:

scipy.stats.logrank(x, y, alternative='two-sided')#

通过对数秩检验比较两个样本的生存分布。

参数 ：：

x, y： 数组 或 CensoredData

根据经验生存函数进行比较的样本。

alternative： {‘双面’，‘less’, ‘greater’}，可选

定义备择假设。

原假设是两个组(例如 X 和 Y)的生存分布是相同的。

以下替代假设 [4] 可用(默认为“双面”)：

• “双面”：两组的生存分布不相同。

• ‘less’：X组的生存受到青睐：X组的故障率函数有时小于Y组的故障率函数。

• ‘greater’：Y组的生存受到青睐：X组的故障率函数有时大于Y组的故障率函数。

返回 ：：

res： LogRankResult

包含属性的对象：

统计 浮点数数组

计算的统计量(定义如下)。它的大小是大多数其他对数秩测试实现返回的大小的平方根。

p值 浮点数数组

测试的计算 p 值。

注意：

对数秩检验 [1] 在两个样本来自同一分布的原假设下，将观察到的事件数与预期事件数进行比较。统计数据是

\[Z_i = \frac{\sum_{j=1}^J(O_{i,j}-E_{i,j})}{\sqrt{\sum_{j=1}^J V_{i,j}}} \rightarrow \mathcal{N}(0,1)\]

其中

\[E_{i,j} = O_j \frac{N_{i,j}}{N_j}, \qquad V_{i,j} = E_{i,j} \left(\frac{N_j-O_j}{N_j}\right) \left(\frac{N_j-N_{i,j}}{N_j-1}\right),\]

\(i\) 表示组(即，它可以采用值 \(x\) 或 \(y\) ，或者可以省略引用组合样本) \(j\) 表示时间(事件发生的时间)，\(N\) 是事件发生前处于危险中的受试者数量，\(O\) 是当时观察到的事件数量。

logrank 返回的 statistic \(Z_x\) 是许多其他实现返回的统计信息的(带符号)平方根。在零假设下，\(Z_x**2\) 根据一个自由度的卡方分布渐近分布。因此，\(Z_x\) 根据标准正态分布渐近分布。使用 \(Z_x\) 的优点是保留了符号信息(即观察到的事件数量是否倾向于小于或大于原假设下的预期数量)，从而允许 scipy.stats.logrank 提供单方面的替代假设。

参考：

[1]

Mantel N.“生存数据的评估和考虑中出现的两个新的排名顺序统计数据。”癌症化疗报告，50(3):163-170，PMID：5910392，1966

[2]

布兰德·奥特曼，“The logrank test”，BMJ，328:1073，DOI:10.1136/bmj.328.7447.1073，2004 年

[3]

“Logrank test”，维基百科，https://en.wikipedia.org/wiki/Logrank_test

[4]

布朗、马克. “关于对数秩检验的方差选择。”生物计量学 71.1 (1984)：65-74。

[5]

约翰·P·克莱因 (Klein) 和梅尔文·L·莫施伯格 (Melvin L. Moeschberger)。生存分析：审查和截断数据的技术。卷。 1230.纽约：施普林格，2003年。

例子：

参考文献[2]比较了两种不同类型的复发性恶性胶质瘤患者的生存时间。下面的样本记录了每位患者参与研究的时间(周数)。使用 scipy.stats.CensoredData 类是因为数据是right-censored：未经审查的观察结果与观察到的死亡相对应，而审查的观察结果与因其他原因离开研究的患者相对应。

>>> from scipy import stats
>>> x = stats.CensoredData(
...     uncensored=[6, 13, 21, 30, 37, 38, 49, 50,
...                 63, 79, 86, 98, 202, 219],
...     right=[31, 47, 80, 82, 82, 149]
... )
>>> y = stats.CensoredData(
...     uncensored=[10, 10, 12, 13, 14, 15, 16, 17, 18, 20, 24, 24,
...                 25, 28,30, 33, 35, 37, 40, 40, 46, 48, 76, 81,
...                 82, 91, 112, 181],
...     right=[34, 40, 70]
... )

我们可以计算并可视化两组的经验生存函数，如下所示。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> ax = plt.subplot()
>>> ecdf_x = stats.ecdf(x)
>>> ecdf_x.sf.plot(ax, label='Astrocytoma')
>>> ecdf_y = stats.ecdf(y)
>>> ecdf_x.sf.plot(ax, label='Glioblastoma')
>>> ax.set_xlabel('Time to death (weeks)')
>>> ax.set_ylabel('Empirical SF')
>>> plt.legend()
>>> plt.show()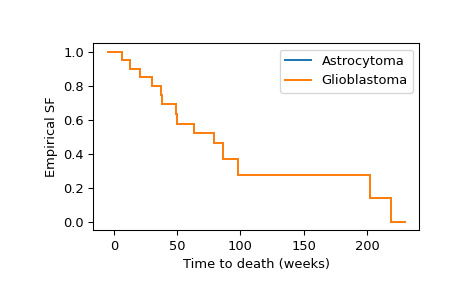

对经验生存函数的目视检查表明，两组之间的生存时间往往不同。为了正式评估差异在 1% 水平上是否显著，我们使用对数秩检验。

>>> res = stats.logrank(x=x, y=y)
>>> res.statistic
-2.73799...
>>> res.pvalue
0.00618...

p 值小于 1%，因此我们可以将这些数据视为反对原假设的证据，支持两个生存函数之间存在差异的替代方案。