Python SciPy stats.invwishart用法及代码示例

本文简要介绍 python 语言中 scipy.stats.invwishart 的用法。

用法:

scipy.stats.invwishart = <scipy.stats._multivariate.invwishart_gen object>#

逆 Wishart 随机变量。

df 关键字指定自由度。 scale 关键字指定比例矩阵，它必须是对称且正定的。在这种情况下，尺度矩阵通常被解释为多元正态协方差矩阵。

参数 ：：

df： int

自由度，必须大于或等于尺度矩阵的维度

scale： array_like

分布的对称正定尺度矩阵

seed： {无，int，np.random.RandomState，np.random.Generator}，可选

用于绘制随机变量。如果种子是None， 这RandomState使用单例。如果种子是一个 int，一个新的RandomState使用实例，用种子播种。如果种子已经是一个RandomState或者Generator实例，然后使用该对象。默认为None.

抛出 ：：

scipy.linalg.LinAlgError

如果尺度矩阵尺度不是正定的。

注意：

尺度矩阵scale必须是对称正定矩阵。不支持奇异矩阵，包括对称正半定情况。不检查对称性；仅使用下三角形部分。

逆 Wishart 分布通常表示为

\[W_p^{-1}(\nu, \Psi)\]

其中\(\nu\) 是自由度，\(\Psi\) 是\(p \times p\) 比例矩阵。

invwishart 的概率密度函数支持正定矩阵 \(S\) ；如果\(S \sim W^{-1}_p(\nu, \Sigma)\)，则其PDF由下式给出：

\[f(S) = \frac{|\Sigma|^\frac{\nu}{2}}{2^{ \frac{\nu p}{2} } |S|^{\frac{\nu + p + 1}{2}} \Gamma_p \left(\frac{\nu}{2} \right)} \exp\left( -tr(\Sigma S^{-1}) / 2 \right)\]

如果\(S \sim W_p^{-1}(\nu, \Psi)\)(逆Wishart)然后\(S^{-1} \sim W_p(\nu, \Psi^{-1})\)(Wishart)。

如果比例矩阵是一维且等于 1，则逆 Wishart 分布 \(W_1(\nu, 1)\) 折叠为参数 shape = \(\frac{\nu}{2}\) 和 scale = \(\frac{1}{2}\) 的逆 Gamma 分布。

参考：

[1]

M.L.伊顿，“多元统计：向量空间方法”，威利，1983 年。

[2]

M.C. Jones，“生成逆 Wishart 矩阵”，统计通信 - 模拟和计算，第一卷。 14.2，第 511-514 页，1985 年。

[3]

Gupta, M. 和 Srivastava, S.“微分熵和相对熵的参数贝叶斯估计”。熵 12, 818 - 843。2010。

例子：

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.stats import invwishart, invgamma
>>> x = np.linspace(0.01, 1, 100)
>>> iw = invwishart.pdf(x, df=6, scale=1)
>>> iw[:3]
array([  1.20546865e-15,   5.42497807e-06,   4.45813929e-03])
>>> ig = invgamma.pdf(x, 6/2., scale=1./2)
>>> ig[:3]
array([  1.20546865e-15,   5.42497807e-06,   4.45813929e-03])
>>> plt.plot(x, iw)
>>> plt.show()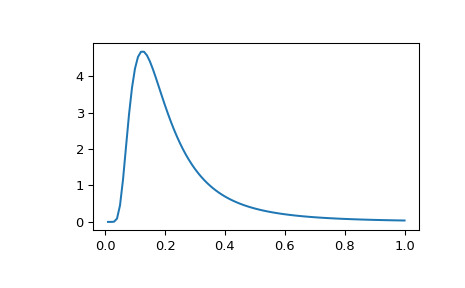

输入分位数可以是任何形状的数组，只要最后一个轴标记组件即可。

或者，可以调用对象(作为函数)来固定自由度和尺度参数，返回 “frozen” 逆 Wishart 随机变量：

>>> rv = invwishart(df=1, scale=1)
>>> # Frozen object with the same methods but holding the given
>>> # degrees of freedom and scale fixed.