本文简要介绍 python 语言中 scipy.stats.mielke 的用法。
用法:
scipy.stats.mielke = <scipy.stats._continuous_distns.mielke_gen object>#Mielke Beta-Kappa /Dagum 连续随机变量。
作为
rv_continuous类的实例,mielke对象从它继承了一组通用方法(完整列表见下文),并用特定于此特定发行版的详细信息来完成它们。注意:
mielke的概率密度函数为:对于 和 。该分布有时称为 Dagum 分布 ([2])。它已在 [3] 中定义,称为 Burr III 型分布(带有参数
c=s和d=k/s的burr)。mielke将k和s作为形状参数。上面的概率密度在“standardized” 表格中定义。要移动和/或缩放分布,请使用
loc和scale参数。具体来说,mielke.pdf(x, k, s, loc, scale)等同于mielke.pdf(y, k, s) / scale和y = (x - loc) / scale。请注意,移动分布的位置不会使其成为“noncentral” 分布;某些分布的非中心概括可在单独的类中获得。参考:
[1]Mielke, P.W.,1973 年“用于说明和分析降水数据的另一类分布”。 J.应用。流星, 12, 275-280
[2]Dagum, C.,1977 年“个人收入分配的新模式”。经济贴花,33, 327-367。
[3]Burr, I. W. “Cumulative frequency functions”,《数理统计年鉴》,13(2),第 215-232 页 (1942)。
例子:
>>> import numpy as np >>> from scipy.stats import mielke >>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots(1, 1)计算前四个时刻:
>>> k, s = 10.4, 4.6 >>> mean, var, skew, kurt = mielke.stats(k, s, moments='mvsk')显示概率密度函数(
pdf):>>> x = np.linspace(mielke.ppf(0.01, k, s), ... mielke.ppf(0.99, k, s), 100) >>> ax.plot(x, mielke.pdf(x, k, s), ... 'r-', lw=5, alpha=0.6, label='mielke pdf')或者,可以调用分布对象(作为函数)来固定形状、位置和比例参数。这将返回一个 “frozen” RV 对象,其中包含固定的给定参数。
冻结分布并显示冻结的
pdf:>>> rv = mielke(k, s) >>> ax.plot(x, rv.pdf(x), 'k-', lw=2, label='frozen pdf')检查
cdf和ppf的准确性:>>> vals = mielke.ppf([0.001, 0.5, 0.999], k, s) >>> np.allclose([0.001, 0.5, 0.999], mielke.cdf(vals, k, s)) True生成随机数:
>>> r = mielke.rvs(k, s, size=1000)并比较直方图:
>>> ax.hist(r, density=True, bins='auto', histtype='stepfilled', alpha=0.2) >>> ax.set_xlim([x[0], x[-1]]) >>> ax.legend(loc='best', frameon=False) >>> plt.show()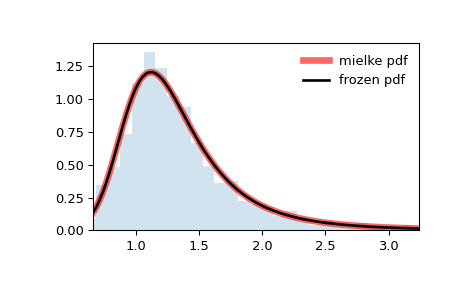
相关用法
- Python SciPy stats.median_abs_deviation用法及代码示例
- Python SciPy stats.multiscale_graphcorr用法及代码示例
- Python SciPy stats.multivariate_normal用法及代码示例
- Python SciPy stats.multivariate_hypergeom用法及代码示例
- Python SciPy stats.mode用法及代码示例
- Python SciPy stats.monte_carlo_test用法及代码示例
- Python SciPy stats.multivariate_t用法及代码示例
- Python SciPy stats.matrix_normal用法及代码示例
- Python SciPy stats.mood用法及代码示例
- Python SciPy stats.moyal用法及代码示例
- Python SciPy stats.maxwell用法及代码示例
- Python SciPy stats.mvsdist用法及代码示例
- Python SciPy stats.moment用法及代码示例
- Python SciPy stats.multinomial用法及代码示例
- Python SciPy stats.median_absolute_deviation用法及代码示例
- Python SciPy stats.median_test用法及代码示例
- Python SciPy stats.mannwhitneyu用法及代码示例
- Python SciPy stats.anderson用法及代码示例
- Python SciPy stats.iqr用法及代码示例
- Python SciPy stats.genpareto用法及代码示例
- Python SciPy stats.skewnorm用法及代码示例
- Python SciPy stats.cosine用法及代码示例
- Python SciPy stats.norminvgauss用法及代码示例
- Python SciPy stats.directional_stats用法及代码示例
- Python SciPy stats.invwishart用法及代码示例
注:本文由纯净天空筛选整理自scipy.org大神的英文原创作品 scipy.stats.mielke。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
