本文简要介绍 python 语言中 scipy.stats.monte_carlo_test 的用法。
用法:
scipy.stats.monte_carlo_test(data, rvs, statistic, *, vectorized=None, n_resamples=9999, batch=None, alternative='two-sided', axis=0)#执行蒙特卡罗假设检验。
数据包含一个样本或一个或多个样本的序列。 rvs 指定原假设下数据中样本的分布。将给定数据的统计值与蒙特卡洛零分布进行比较:使用 rvs 生成的每个 n_resamples 样本集的统计值。这给出了 p 值,即在原假设下观察到检验统计量的极值的概率。
- data: 类似数组或类似数组的序列
观察值数组或数组序列。
- rvs: 可调用或可调用元组
在原假设下生成随机变量的可调用对象或可调用对象序列。的每个元素房车必须是接受关键字参数的可调用对象
size(例如:rvs(size=(m, n)))并返回该形状的 N-d 数组样本。如果房车是一个序列,其中可调用的数量房车必须与样本数相匹配数据, IE。len(rvs) == len(data).如果房车是一个可调用的,数据被视为单个样本。- statistic: 可调用的
要计算假设检验 p 值的统计量。统计必须是接受样本的可调用对象(例如
statistic(sample)) 或者len(rvs)单独的样本(例如statistic(samples1, sample2)如果房车包含两个可调用对象和数据包含两个样本)并返回结果统计数据。如果矢量化已设置True,统计还必须接受关键字参数轴并被矢量化以计算沿提供的统计量轴中的样本数数据.- vectorized: 布尔型,可选
如果矢量化已设置
False,统计不会传递关键字参数轴并且预计仅计算一维样本的统计量。如果True,统计将传递关键字参数轴并预计将计算统计数据轴当传递 ND 样本数组时。如果None(默认),矢量化将被设置True如果axis是一个参数统计。使用矢量化统计通常可以减少计算时间。- n_resamples: 整数,默认值:9999
从 rvs 的每个可调用对象中抽取的样本数。等效地,零假设下的数量统计值用作蒙特卡罗零分布。
- batch: 整数,可选
每次调用时要处理的蒙特卡罗样本数统计.内存使用量为 O(批*
sample.size[axis])。默认为None, 在这种情况下批等于n_resamples.- alternative: {‘双面’,‘less’, ‘greater’}
计算 p 值的备择假设。对于每个备选方案,p 值定义如下。
'greater':大于或等于检验统计量观察值的空分布百分比。'less':小于或等于检验统计量观察值的空分布百分比。'two-sided':上述 p 值中较小值的两倍。
- axis: 整数,默认值:0
用于计算统计数据的数据轴(或数据中的每个样本)。
- res: MonteCarloTestResult
具有属性的对象:
- 统计 浮点数或 ndarray
观测数据的检验统计量。
- p值 浮点数或 ndarray
给定替代方案的 p 值。
- null_distribution ndarray
在原假设下生成的检验统计量的值。
参数 ::
返回 ::
参考:
[1]B. Phipson 和 G. K. Smyth。 “排列 P 值不应该为零:随机抽取排列时计算精确的 P 值。”遗传学和分子生物学中的统计应用 9.1 (2010)。
例子:
假设我们希望测试是否从正态分布中抽取了一个小样本。我们决定使用样本的偏度作为检验统计量,并且我们将认为 0.05 的 p 值具有统计显著性。
>>> import numpy as np >>> from scipy import stats >>> def statistic(x, axis): ... return stats.skew(x, axis)收集数据后,我们计算检验统计量的观察值。
>>> rng = np.random.default_rng() >>> x = stats.skewnorm.rvs(a=1, size=50, random_state=rng) >>> statistic(x, axis=0) 0.12457412450240658为了确定从正态分布中抽取样本时偶然观察到偏度极值的概率,我们可以执行蒙特卡罗假设检验。该检验将从正态分布中随机抽取许多样本,计算每个样本的偏度,并将原始偏度与该分布进行比较,以确定近似的 p 值。
>>> from scipy.stats import monte_carlo_test >>> # because our statistic is vectorized, we pass `vectorized=True` >>> rvs = lambda size: stats.norm.rvs(size=size, random_state=rng) >>> res = monte_carlo_test(x, rvs, statistic, vectorized=True) >>> print(res.statistic) 0.12457412450240658 >>> print(res.pvalue) 0.7012在零假设下获得小于或等于观测值的检验统计量的概率约为 70%。这大于我们选择的 5% 阈值,因此我们不能认为这是反对原假设的重要证据。
请注意,此 p 值本质上与
scipy.stats.skewtest的 p 值匹配,后者依赖于基于样本偏度的检验统计量的渐近分布。>>> stats.skewtest(x).pvalue 0.6892046027110614此渐近近似对于小样本量无效,但
monte_carlo_test可用于任何大小的样本。>>> x = stats.skewnorm.rvs(a=1, size=7, random_state=rng) >>> # stats.skewtest(x) would produce an error due to small sample >>> res = monte_carlo_test(x, rvs, statistic, vectorized=True)提供检验统计量的蒙特卡罗分布以供进一步研究。
>>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots() >>> ax.hist(res.null_distribution, bins=50) >>> ax.set_title("Monte Carlo distribution of test statistic") >>> ax.set_xlabel("Value of Statistic") >>> ax.set_ylabel("Frequency") >>> plt.show()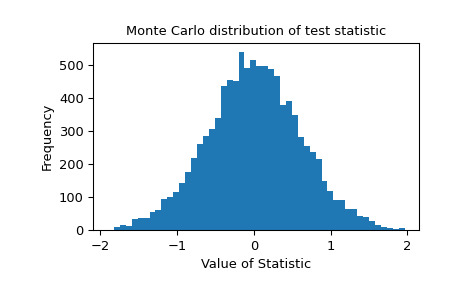
相关用法
- Python SciPy stats.mode用法及代码示例
- Python SciPy stats.mood用法及代码示例
- Python SciPy stats.moyal用法及代码示例
- Python SciPy stats.moment用法及代码示例
- Python SciPy stats.median_abs_deviation用法及代码示例
- Python SciPy stats.multiscale_graphcorr用法及代码示例
- Python SciPy stats.multivariate_normal用法及代码示例
- Python SciPy stats.multivariate_hypergeom用法及代码示例
- Python SciPy stats.multivariate_t用法及代码示例
- Python SciPy stats.matrix_normal用法及代码示例
- Python SciPy stats.maxwell用法及代码示例
- Python SciPy stats.mvsdist用法及代码示例
- Python SciPy stats.multinomial用法及代码示例
- Python SciPy stats.mielke用法及代码示例
- Python SciPy stats.median_absolute_deviation用法及代码示例
- Python SciPy stats.median_test用法及代码示例
- Python SciPy stats.mannwhitneyu用法及代码示例
- Python SciPy stats.anderson用法及代码示例
- Python SciPy stats.iqr用法及代码示例
- Python SciPy stats.genpareto用法及代码示例
- Python SciPy stats.skewnorm用法及代码示例
- Python SciPy stats.cosine用法及代码示例
- Python SciPy stats.norminvgauss用法及代码示例
- Python SciPy stats.directional_stats用法及代码示例
- Python SciPy stats.invwishart用法及代码示例
注:本文由纯净天空筛选整理自scipy.org大神的英文原创作品 scipy.stats.monte_carlo_test。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
