本文簡要介紹 python 語言中 scipy.stats.monte_carlo_test 的用法。
用法:
scipy.stats.monte_carlo_test(data, rvs, statistic, *, vectorized=None, n_resamples=9999, batch=None, alternative='two-sided', axis=0)#執行蒙特卡羅假設檢驗。
數據包含一個樣本或一個或多個樣本的序列。 rvs 指定原假設下數據中樣本的分布。將給定數據的統計值與蒙特卡洛零分布進行比較:使用 rvs 生成的每個 n_resamples 樣本集的統計值。這給出了 p 值,即在原假設下觀察到檢驗統計量的極值的概率。
- data: 類似數組或類似數組的序列
觀察值數組或數組序列。
- rvs: 可調用或可調用元組
在原假設下生成隨機變量的可調用對象或可調用對象序列。的每個元素房車必須是接受關鍵字參數的可調用對象
size(例如:rvs(size=(m, n)))並返回該形狀的 N-d 數組樣本。如果房車是一個序列,其中可調用的數量房車必須與樣本數相匹配數據, IE。len(rvs) == len(data).如果房車是一個可調用的,數據被視為單個樣本。- statistic: 可調用的
要計算假設檢驗 p 值的統計量。統計必須是接受樣本的可調用對象(例如
statistic(sample)) 或者len(rvs)單獨的樣本(例如statistic(samples1, sample2)如果房車包含兩個可調用對象和數據包含兩個樣本)並返回結果統計數據。如果矢量化已設置True,統計還必須接受關鍵字參數軸並被矢量化以計算沿提供的統計量軸中的樣本數數據.- vectorized: 布爾型,可選
如果矢量化已設置
False,統計不會傳遞關鍵字參數軸並且預計僅計算一維樣本的統計量。如果True,統計將傳遞關鍵字參數軸並預計將計算統計數據軸當傳遞 ND 樣本數組時。如果None(默認),矢量化將被設置True如果axis是一個參數統計。使用矢量化統計通常可以減少計算時間。- n_resamples: 整數,默認值:9999
從 rvs 的每個可調用對象中抽取的樣本數。等效地,零假設下的數量統計值用作蒙特卡羅零分布。
- batch: 整數,可選
每次調用時要處理的蒙特卡羅樣本數統計.內存使用量為 O(批*
sample.size[axis])。默認為None, 在這種情況下批等於n_resamples.- alternative: {‘雙麵’,‘less’, ‘greater’}
計算 p 值的備擇假設。對於每個備選方案,p 值定義如下。
'greater':大於或等於檢驗統計量觀察值的空分布百分比。'less':小於或等於檢驗統計量觀察值的空分布百分比。'two-sided':上述 p 值中較小值的兩倍。
- axis: 整數,默認值:0
用於計算統計數據的數據軸(或數據中的每個樣本)。
- res: MonteCarloTestResult
具有屬性的對象:
- 統計 浮點數或 ndarray
觀測數據的檢驗統計量。
- p值 浮點數或 ndarray
給定替代方案的 p 值。
- null_distribution ndarray
在原假設下生成的檢驗統計量的值。
參數 ::
返回 ::
參考:
[1]B. Phipson 和 G. K. Smyth。 “排列 P 值不應該為零:隨機抽取排列時計算精確的 P 值。”遺傳學和分子生物學中的統計應用 9.1 (2010)。
例子:
假設我們希望測試是否從正態分布中抽取了一個小樣本。我們決定使用樣本的偏度作為檢驗統計量,並且我們將認為 0.05 的 p 值具有統計顯著性。
>>> import numpy as np >>> from scipy import stats >>> def statistic(x, axis): ... return stats.skew(x, axis)收集數據後,我們計算檢驗統計量的觀察值。
>>> rng = np.random.default_rng() >>> x = stats.skewnorm.rvs(a=1, size=50, random_state=rng) >>> statistic(x, axis=0) 0.12457412450240658為了確定從正態分布中抽取樣本時偶然觀察到偏度極值的概率,我們可以執行蒙特卡羅假設檢驗。該檢驗將從正態分布中隨機抽取許多樣本,計算每個樣本的偏度,並將原始偏度與該分布進行比較,以確定近似的 p 值。
>>> from scipy.stats import monte_carlo_test >>> # because our statistic is vectorized, we pass `vectorized=True` >>> rvs = lambda size: stats.norm.rvs(size=size, random_state=rng) >>> res = monte_carlo_test(x, rvs, statistic, vectorized=True) >>> print(res.statistic) 0.12457412450240658 >>> print(res.pvalue) 0.7012在零假設下獲得小於或等於觀測值的檢驗統計量的概率約為 70%。這大於我們選擇的 5% 閾值,因此我們不能認為這是反對原假設的重要證據。
請注意,此 p 值本質上與
scipy.stats.skewtest的 p 值匹配,後者依賴於基於樣本偏度的檢驗統計量的漸近分布。>>> stats.skewtest(x).pvalue 0.6892046027110614此漸近近似對於小樣本量無效,但
monte_carlo_test可用於任何大小的樣本。>>> x = stats.skewnorm.rvs(a=1, size=7, random_state=rng) >>> # stats.skewtest(x) would produce an error due to small sample >>> res = monte_carlo_test(x, rvs, statistic, vectorized=True)提供檢驗統計量的蒙特卡羅分布以供進一步研究。
>>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots() >>> ax.hist(res.null_distribution, bins=50) >>> ax.set_title("Monte Carlo distribution of test statistic") >>> ax.set_xlabel("Value of Statistic") >>> ax.set_ylabel("Frequency") >>> plt.show()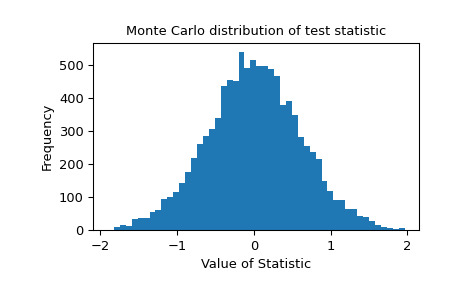
相關用法
- Python SciPy stats.mode用法及代碼示例
- Python SciPy stats.mood用法及代碼示例
- Python SciPy stats.moyal用法及代碼示例
- Python SciPy stats.moment用法及代碼示例
- Python SciPy stats.median_abs_deviation用法及代碼示例
- Python SciPy stats.multiscale_graphcorr用法及代碼示例
- Python SciPy stats.multivariate_normal用法及代碼示例
- Python SciPy stats.multivariate_hypergeom用法及代碼示例
- Python SciPy stats.multivariate_t用法及代碼示例
- Python SciPy stats.matrix_normal用法及代碼示例
- Python SciPy stats.maxwell用法及代碼示例
- Python SciPy stats.mvsdist用法及代碼示例
- Python SciPy stats.multinomial用法及代碼示例
- Python SciPy stats.mielke用法及代碼示例
- Python SciPy stats.median_absolute_deviation用法及代碼示例
- Python SciPy stats.median_test用法及代碼示例
- Python SciPy stats.mannwhitneyu用法及代碼示例
- Python SciPy stats.anderson用法及代碼示例
- Python SciPy stats.iqr用法及代碼示例
- Python SciPy stats.genpareto用法及代碼示例
- Python SciPy stats.skewnorm用法及代碼示例
- Python SciPy stats.cosine用法及代碼示例
- Python SciPy stats.norminvgauss用法及代碼示例
- Python SciPy stats.directional_stats用法及代碼示例
- Python SciPy stats.invwishart用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.stats.monte_carlo_test。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
