本文简要介绍 python 语言中 scipy.stats.multivariate_t 的用法。
用法:
scipy.stats.multivariate_t = <scipy.stats._multivariate.multivariate_t_gen object>#多变量t-distributed 随机变量。
loc 参数指定位置。 shape 参数指定半正定形状矩阵。 df 参数指定自由度。
除了调用下面的方法外,对象本身也可以作为函数调用,以固定位置、形状矩阵和自由度参数,返回 “frozen” 多元 t 分布随机数。
- loc: 数组,可选
分布的位置。 (默认
0)- shape: 数组,可选
分布的半正定矩阵。 (默认
1)- df: 浮点数,可选
分配的自由度;必须大于零。如果
np.inf则结果为多元正态。默认值为1。- allow_singular: 布尔型,可选
是否允许奇异矩阵。 (默认
False)- seed: {无,int,np.random.RandomState,np.random.Generator},可选
用于绘制随机变量。如果种子是None, 这RandomState使用单例。如果种子是一个 int,一个新的
RandomState使用实例,用种子播种。如果种子已经是一个RandomState或者Generator实例,然后使用该对象。默认为None.
参数 ::
注意:
设置参数位置到
None相当于拥有位置成为zero-vector。参数形状可以是标量,在这种情况下,形状矩阵是该值的单位乘以,形状矩阵的对角线元素的向量,或二维 数组。矩阵形状必须是(对称)半正定矩阵。的行列式和倒数形状分别计算为 pseudo-determinant 和 pseudo-inverse,因此形状不需要满级。multivariate_t的概率密度函数为其中 是 的维度, 是 维位置, 维形状矩阵, 是自由度。
参考:
[1]Arellano-Valle等。 “多元 Skew-Elliptical 分布的香农熵和互信息”。斯堪的纳维亚统计杂志。卷。 40,第 1 期。
例子:
可以调用该对象(作为函数)来修复 loc、shape、df 和 allow_singular 参数,返回 “frozen” multivariate_t 随机变量:
>>> import numpy as np >>> from scipy.stats import multivariate_t >>> rv = multivariate_t([1.0, -0.5], [[2.1, 0.3], [0.3, 1.5]], df=2) >>> # Frozen object with the same methods but holding the given location, >>> # scale, and degrees of freedom fixed.创建 PDF 的等高线图。
>>> import matplotlib.pyplot as plt >>> x, y = np.mgrid[-1:3:.01, -2:1.5:.01] >>> pos = np.dstack((x, y)) >>> fig, ax = plt.subplots(1, 1) >>> ax.set_aspect('equal') >>> plt.contourf(x, y, rv.pdf(pos))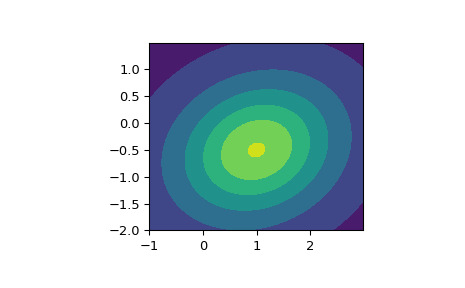
相关用法
- Python SciPy stats.multivariate_normal用法及代码示例
- Python SciPy stats.multivariate_hypergeom用法及代码示例
- Python SciPy stats.multiscale_graphcorr用法及代码示例
- Python SciPy stats.multinomial用法及代码示例
- Python SciPy stats.median_abs_deviation用法及代码示例
- Python SciPy stats.mode用法及代码示例
- Python SciPy stats.monte_carlo_test用法及代码示例
- Python SciPy stats.matrix_normal用法及代码示例
- Python SciPy stats.mood用法及代码示例
- Python SciPy stats.moyal用法及代码示例
- Python SciPy stats.maxwell用法及代码示例
- Python SciPy stats.mvsdist用法及代码示例
- Python SciPy stats.moment用法及代码示例
- Python SciPy stats.mielke用法及代码示例
- Python SciPy stats.median_absolute_deviation用法及代码示例
- Python SciPy stats.median_test用法及代码示例
- Python SciPy stats.mannwhitneyu用法及代码示例
- Python SciPy stats.anderson用法及代码示例
- Python SciPy stats.iqr用法及代码示例
- Python SciPy stats.genpareto用法及代码示例
- Python SciPy stats.skewnorm用法及代码示例
- Python SciPy stats.cosine用法及代码示例
- Python SciPy stats.norminvgauss用法及代码示例
- Python SciPy stats.directional_stats用法及代码示例
- Python SciPy stats.invwishart用法及代码示例
注:本文由纯净天空筛选整理自scipy.org大神的英文原创作品 scipy.stats.multivariate_t。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
