Python SciPy stats.kendalltau用法及代码示例

本文简要介绍 python 语言中 scipy.stats.kendalltau 的用法。

用法:

scipy.stats.kendalltau(x, y, *, initial_lexsort=<object object>, nan_policy='propagate', method='auto', variant='b', alternative='two-sided')#

计算 Kendall 的 tau，这是一种序数数据的相关性度量。

Kendall tau 是衡量两个排名之间对应关系的指标。接近 1 的值表示强烈同意，接近 -1 的值表示强烈反对。这实现了 Kendall tau 的两个变体：tau-b(默认)和 tau-c(也称为 Stuart 的 tau-c)。它们的区别仅在于如何将它们归一化到 -1 到 1 的范围内；假设检验(它们的 p 值)是相同的。 Kendall 最初的tau-a 没有单独实现，因为tau-b 和tau-c 在没有联系的情况下都减少为tau-a。

参数 ：：

x, y： array_like

排列的数组，形状相同。如果数组不是一维的，它们将被展平为一维。

initial_lexsort： 布尔值，可选，已弃用

该参数未使用。

nan_policy： {‘propagate’, ‘raise’, ‘omit’}，可选

定义当输入包含 nan 时如何处理。以下选项可用(默认为‘propagate’)：

• ‘propagate’: returns nan

• ‘raise’: throws an error

• ‘omit’: performs the calculations ignoring nan values

method： {‘auto’, ‘asymptotic’, ‘exact’}，可选

定义使用哪种方法来计算 p 值 [5]。以下选项可用(默认为‘auto’)：

• ‘auto’: selects the appropriate method based on a trade-off between speed and accuracy

• ‘asymptotic’: uses a normal approximation valid for large samples

• ‘exact’: computes the exact p-value, but can only be used if no ties are present. As the sample size increases, the ‘exact’ computation time may grow and the result may lose some precision.

variant： {‘b’, ‘c’}，可选

定义返回 Kendall tau 的哪个变体。默认为‘b’。

alternative： {‘双面’，‘less’, ‘greater’}，可选

定义备择假设。默认为“双面”。可以使用以下选项：

• “双边”：等级相关性非零

• ‘less’：秩相关为负(小于零)

• ‘greater’：秩相关为正(大于零)

返回 ：：

res： SignificanceResult

包含属性的对象：

统计 浮点数

tau 统计量。

p值 浮点数

假设检验的 p 值，其原假设是不存在关联，tau = 0。

注意：

使用的 Kendall tau 定义为 [2]：

tau_b = (P - Q) / sqrt((P + Q + T) * (P + Q + U))

tau_c = 2 (P - Q) / (n**2 * (m - 1) / m)

其中 P 是一致对的数量，Q 是不一致对的数量，T 是仅在 x 中的关系数，而 U 是仅在 y 中的关系数。如果同一对在 x 和 y 中出现平局，则不会将其添加到 T 或 U。n 是样本总数，m 是 x 或 y 中唯一值的数量，以较小者为准。

参考：

[1]

Maurice G. Kendall，“等级相关性的新度量”，Biometrika Vol。 30，第 1/2 期，第 81-93 页，1938 年。

[2]

Maurice G. Kendall，“排名问题中关系的处理”，Biometrika Vol。 33，第 3 期，第 239-251 页。 1945 年。

[3]

Gottfried E. Noether，“非参数统计要素”，John Wiley & Sons，1967 年。

[4]

Peter M. Fenwick，“累积频率表的新数据结构”，软件：实践与经验，卷。 24，第 3 期，第 327-336 页，1994 年。

[5]

Maurice G. Kendall，“Rank Correlation Methods”(第 4 版)，Charles Griffin & Co.，1970 年。

[6]

Kershenobich, D.、Fierro, F. J. 和 Rojkind, M. (1970)。人肝硬化中游离脯氨酸池与胶原蛋白含量的关系。临床研究杂志，49(12), 2246-2249。

[7]

Hollander, M.、Wolfe, D. A. 和 Chicken, E. (2013)。非参数统计方法。约翰·威利父子。

[8]

B. Phipson 和 G. K. Smyth。 “排列 P 值不应该为零：随机抽取排列时计算精确的 P 值。”遗传学和分子生物学中的统计应用 9.1 (2010)。

例子：

考虑以下来自[6]的数据，该数据研究了不健康人类肝脏中游离脯氨酸(一种氨基酸)和总胶原蛋白(一种常见于结缔组织中的蛋白质)之间的关系。

下面的x 和y 数组记录了两种化合物的测量值。观察结果是配对的：每个游离脯氨酸测量值均取自同一肝脏，作为相同index下的总胶原蛋白测量值。

>>> import numpy as np
>>> # total collagen (mg/g dry weight of liver)
>>> x = np.array([7.1, 7.1, 7.2, 8.3, 9.4, 10.5, 11.4])
>>> # free proline (μ mole/g dry weight of liver)
>>> y = np.array([2.8, 2.9, 2.8, 2.6, 3.5, 4.6, 5.0])

[7] 使用 Spearman 相关系数对这些数据进行了分析，该统计量与 Kendall tau 类似，因为它对样本之间的序数相关性也很敏感。让我们使用 Kendall 的 tau 蛋白进行类似的研究。

>>> from scipy import stats
>>> res = stats.kendalltau(x, y)
>>> res.statistic
0.5499999999999999

对于具有强正序相关的样本，该统计量的值往往较高(接近 1)；对于具有强负序相关的样本，该统计量的值往往较低(接近 -1)；对于具有强负序相关的样本，该统计量的值往往较小(接近于 0)。具有弱序数相关性。

该检验是通过将统计观察值与零分布进行比较来进行的：零假设下得出的统计值分布，即总胶原蛋白和游离脯氨酸测量值是独立的。

对于此测试，没有联系的大样本的零分布近似为具有方差 (2*(2*n + 5))/(9*n*(n - 1)) 的正态分布，其中 n = len(x) 。

>>> import matplotlib.pyplot as plt
>>> n = len(x)  # len(x) == len(y)
>>> var = (2*(2*n + 5))/(9*n*(n - 1))
>>> dist = stats.norm(scale=np.sqrt(var))
>>> z_vals = np.linspace(-1.25, 1.25, 100)
>>> pdf = dist.pdf(z_vals)
>>> fig, ax = plt.subplots(figsize=(8, 5))
>>> def plot(ax):  # we'll re-use this
...     ax.plot(z_vals, pdf)
...     ax.set_title("Kendall Tau Test Null Distribution")
...     ax.set_xlabel("statistic")
...     ax.set_ylabel("probability density")
>>> plot(ax)
>>> plt.show()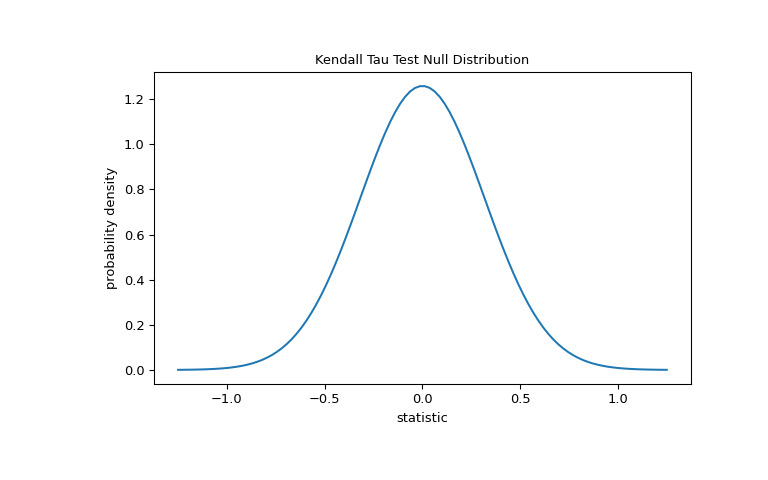

比较通过 p 值进行量化：零分布中比统计观察值极端或更极端的值的比例。在统计量为正的双边测试中，大于转换统计量的零分布元素和小于观察统计量负值的零分布元素均被视为 “more extreme”。

>>> fig, ax = plt.subplots(figsize=(8, 5))
>>> plot(ax)
>>> pvalue = dist.cdf(-res.statistic) + dist.sf(res.statistic)
>>> annotation = (f'p-value={pvalue:.4f}\n(shaded area)')
>>> props = dict(facecolor='black', width=1, headwidth=5, headlength=8)
>>> _ = ax.annotate(annotation, (0.65, 0.15), (0.8, 0.3), arrowprops=props)
>>> i = z_vals >= res.statistic
>>> ax.fill_between(z_vals[i], y1=0, y2=pdf[i], color='C0')
>>> i = z_vals <= -res.statistic
>>> ax.fill_between(z_vals[i], y1=0, y2=pdf[i], color='C0')
>>> ax.set_xlim(-1.25, 1.25)
>>> ax.set_ylim(0, 0.5)
>>> plt.show()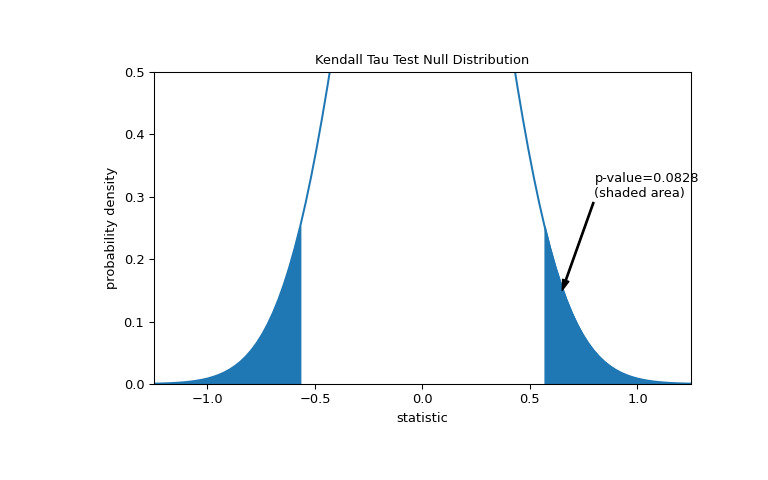

>>> res.pvalue
0.09108705741631495  # approximate p-value

请注意，曲线的阴影区域与 kendalltau 返回的 p 值之间存在轻微差异。这是因为我们的数据具有联系，并且我们忽略了 kendalltau 执行的对零分布方差的联系校正。对于没有联系的样本，绘图的阴影区域和 kendalltau 返回的 p 值将完全匹配。

如果 p 值为 “small” - 也就是说，如果从产生如此统计量极值的独立分布中采样数据的概率较低 - 这可以作为反对零假设的证据，支持替代方案：总胶原蛋白和游离脯氨酸的分布不是独立的。注意：

• 反之则不成立；也就是说，检验不用于为原假设提供证据。

• 将被视为 “small” 的值的阈值是在分析数据之前应做出的选择 [8]，同时考虑误报(错误地拒绝零假设)和漏报(未能拒绝假设)的风险。错误的原假设)。

• p 值小并不能证明效果大；相反，它们只能为 “significant” 效应提供证据，这意味着它们不太可能在原假设下发生。

对于没有中等尺寸连接的样品，kendalltau可以准确计算 p 值。然而，在有联系的情况下，kendalltau诉诸渐近近似。尽管如此，我们可以使用排列检验来准确计算零分布：在总胶原蛋白和游离脯氨酸是独立的零假设下，每个游离脯氨酸测量值与任何总胶原蛋白测量值都有相同的可能被观察到。因此，我们可以组建一个精确的通过计算之间每个可能的元素配对下的统计量来计算空分布x和y.

>>> def statistic(x):  # explore all possible pairings by permuting `x`
...     return stats.kendalltau(x, y).statistic  # ignore pvalue
>>> ref = stats.permutation_test((x,), statistic,
...                              permutation_type='pairings')
>>> fig, ax = plt.subplots(figsize=(8, 5))
>>> plot(ax)
>>> bins = np.linspace(-1.25, 1.25, 25)
>>> ax.hist(ref.null_distribution, bins=bins, density=True)
>>> ax.legend(['aymptotic approximation\n(many observations)',
...            'exact null distribution'])
>>> plot(ax)
>>> plt.show()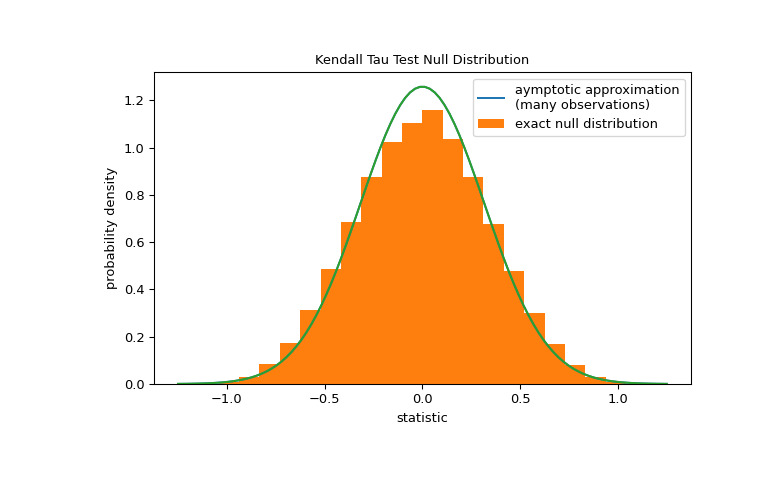

>>> ref.pvalue
0.12222222222222222  # exact p-value

请注意，此处计算的精确 p 值与上面 kendalltau 返回的近似值之间存在显著差异。对于有联系的小样本，请考虑执行排列检验以获得更准确的结果。