Python SciPy stats.kurtosis用法及代码示例

本文简要介绍 python 语言中 scipy.stats.kurtosis 的用法。

用法:

scipy.stats.kurtosis(a, axis=0, fisher=True, bias=True, nan_policy='propagate', *, keepdims=False)#

计算数据集的峰度(Fisher 或 Pearson)。

峰度是第四个中心矩除以方差的平方。如果使用 Fisher 的定义，则从结果中减去 3.0，得到正态分布的 0.0。

如果偏差为 False，则使用 k 统计量计算峰度以消除来自偏差矩估计器的偏差

使用 kurtosistest 查看结果是否足够接近正常。

参数 ：：

a： 数组

计算峰度的数据。

axis： int 或无，默认值：0

如果是 int，则计算统计量的输入轴。输入的每个axis-slice(例如行)的统计信息将出现在输出的相应元素中。如果 None ，输入将在计算统计数据之前被分解。

fisher： 布尔型，可选

如果为 True，则使用 Fisher 的定义(正常 ==> 0.0)。如果为 False，则使用 Pearson 的定义(正常 ==> 3.0)。

bias： 布尔型，可选

如果为 False，则针对统计偏差校正计算。

nan_policy： {‘propagate’, ‘omit’, ‘raise’}

定义如何处理输入 NaN。

• propagate ：如果计算统计数据的轴切片(例如行)中存在NaN，则输出的相应条目将为 NaN。

• omit : 计算时将省略NaNs。如果计算统计数据的轴切片中剩余的数据不足，则输出的相应条目将为 NaN。

• raise ：如果存在 NaN，则会引发 ValueError。

keepdims： 布尔值，默认值：假

如果将其设置为 True，则缩小的轴将作为尺寸为 1 的尺寸留在结果中。使用此选项，结果将针对输入数组正确广播。

返回 ：：

kurtosis： 数组

沿轴的值的峰度，返回 NaN，其中所有值都相等。

注意：

从 SciPy 1.9 开始，np.matrix 输入(不建议用于新代码)在执行计算之前转换为 np.ndarray。在这种情况下，输出将是标量或适当形状的 np.ndarray 而不是 2D np.matrix 。同样，虽然屏蔽数组的屏蔽元素被忽略，但输出将是标量或 np.ndarray 而不是带有 mask=False 的屏蔽数组。

参考：

[1]

Zwillinger, D. 和 Kokoska, S. (2000)。 CRC 标准概率和统计表和公式。查普曼和霍尔：纽约。 2000 年。

例子：

在费舍尔的定义中，正态分布的峰度为零。在以下示例中，峰度接近于零，因为它是根据数据集计算的，而不是根据连续分布计算的。

>>> import numpy as np
>>> from scipy.stats import norm, kurtosis
>>> data = norm.rvs(size=1000, random_state=3)
>>> kurtosis(data)
-0.06928694200380558

具有较高峰度的分布具有较重的尾部。 Fisher 定义中正态分布的零值峰度可以作为参考点。

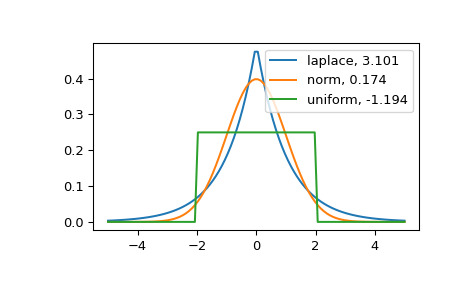
>>> import matplotlib.pyplot as plt
>>> import scipy.stats as stats
>>> from scipy.stats import kurtosis

>>> x = np.linspace(-5, 5, 100)
>>> ax = plt.subplot()
>>> distnames = ['laplace', 'norm', 'uniform']

>>> for distname in distnames:
...     if distname == 'uniform':
...         dist = getattr(stats, distname)(loc=-2, scale=4)
...     else:
...         dist = getattr(stats, distname)
...     data = dist.rvs(size=1000)
...     kur = kurtosis(data, fisher=True)
...     y = dist.pdf(x)
...     ax.plot(x, y, label="{}, {}".format(distname, round(kur, 3)))
...     ax.legend()

拉普拉斯分布的尾部比正态分布重。均匀分布(具有负峰度)的尾部最薄。