本文简要介绍 python 语言中 scipy.special.ive 的用法。
用法:
scipy.special.ive(v, z, out=None) = <ufunc 'ive'>#第一类指数缩放修正贝塞尔函数。
定义为:
ive(v, z) = iv(v, z) * exp(-abs(z.real))对于没有实部的虚数,返回第一类未缩放的贝塞尔函数
iv。- v: 类似浮点数的数组
命令。
- z: 数组 浮点数或复数
争论。
- out: ndarray,可选
函数值的可选输出数组
- 标量或 ndarray
index 缩放的修正贝塞尔函数的值。
参数 ::
返回 ::
注意:
对于正v, AMOS[1] 兹贝西例程被调用。它使用一个功率系列的小z, 大的渐近展开绝对(z),由 Wronskian 和 Neumann 级数归一化的米勒算法用于中间幅度,以及均匀渐近展开和对于大订单。向后递归用于在必要时生成序列或减少订单。
上面的计算是在右半平面上完成的,并通过公式继续到左半平面,
(当 z 的实部为正时有效)。对于负 v,公式
被使用,其中是修改后的第二类贝塞尔函数,使用 AMOS 例程进行评估兹别斯克.
ive对于大型参数很有用z: 对于这些,iv很容易溢出,同时ive不是由于指数缩放。参考:
[1]Donald E. Amos,“AMOS,用于复杂参数和非负阶贝塞尔函数的便携式软件包”,http://netlib.org/amos/
例子:
在以下示例中,
iv返回无穷大,而ive仍返回有限数。>>> from scipy.special import iv, ive >>> import numpy as np >>> import matplotlib.pyplot as plt >>> iv(3, 1000.), ive(3, 1000.) (inf, 0.01256056218254712)通过提供列表或 NumPy 数组作为 v 参数的参数,在某一点评估不同阶数的函数:
>>> ive([0, 1, 1.5], 1.) array([0.46575961, 0.20791042, 0.10798193])通过提供 z 数组,在多个点评估函数的 0 阶。
>>> points = np.array([-2., 0., 3.]) >>> ive(0, points) array([0.30850832, 1. , 0.24300035])通过为 v 和 z 提供数组,在不同阶数的多个点评估函数。两个数组都必须可广播为正确的形状。要计算一维点数组的阶数 0、1 和 2:
>>> ive([[0], [1], [2]], points) array([[ 0.30850832, 1. , 0.24300035], [-0.21526929, 0. , 0.19682671], [ 0.09323903, 0. , 0.11178255]])绘制从 -5 到 5 的 0 到 3 阶函数。
>>> fig, ax = plt.subplots() >>> x = np.linspace(-5., 5., 1000) >>> for i in range(4): ... ax.plot(x, ive(i, x), label=f'$I_{i!r}(z)\cdot e^{{-|z|}}$') >>> ax.legend() >>> ax.set_xlabel(r"$z$") >>> plt.show()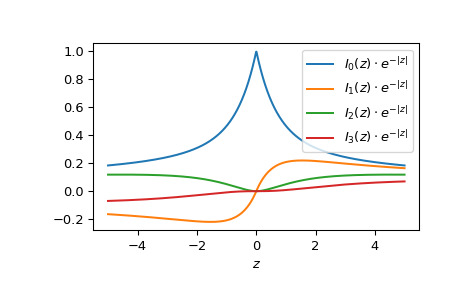
相关用法
- Python SciPy special.ivp用法及代码示例
- Python SciPy special.iv用法及代码示例
- Python SciPy special.i1e用法及代码示例
- Python SciPy special.iti0k0用法及代码示例
- Python SciPy special.it2struve0用法及代码示例
- Python SciPy special.it2i0k0用法及代码示例
- Python SciPy special.itmodstruve0用法及代码示例
- Python SciPy special.inv_boxcox用法及代码示例
- Python SciPy special.i0e用法及代码示例
- Python SciPy special.itstruve0用法及代码示例
- Python SciPy special.it2j0y0用法及代码示例
- Python SciPy special.itj0y0用法及代码示例
- Python SciPy special.itairy用法及代码示例
- Python SciPy special.inv_boxcox1p用法及代码示例
- Python SciPy special.i1用法及代码示例
- Python SciPy special.i0用法及代码示例
- Python SciPy special.exp1用法及代码示例
- Python SciPy special.expn用法及代码示例
- Python SciPy special.ncfdtri用法及代码示例
- Python SciPy special.gamma用法及代码示例
- Python SciPy special.y1用法及代码示例
- Python SciPy special.y0用法及代码示例
- Python SciPy special.ellip_harm_2用法及代码示例
- Python SciPy special.smirnovi用法及代码示例
- Python SciPy special.ker用法及代码示例
注:本文由纯净天空筛选整理自scipy.org大神的英文原创作品 scipy.special.ive。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
