本文简要介绍 python 语言中 scipy.special.eval_legendre 的用法。
用法:
scipy.special.eval_legendre(n, x, out=None) = <ufunc 'eval_legendre'>#在某一点计算勒让德多项式。
Legendre多项式可以通过高斯超几何函数定义为
当 是整数时,结果是度数的多项式 。有关详细信息,请参阅 [AS] 中的 22.5.49。
- n: array_like
多项式的次数。如果不是整数,则通过与高斯超几何函数的关系确定结果。
- x: array_like
计算勒让德多项式的点
- out: ndarray,可选
函数值的可选输出数组
- P: 标量或 ndarray
勒让德多项式的值
参数 ::
返回 ::
参考:
[AS]Milton Abramowitz 和 Irene A. Stegun 合编。带有公式、图表和数学表格的数学函数手册。纽约:多佛,1972 年。
例子:
>>> import numpy as np >>> from scipy.special import eval_legendre在 x = 0 处计算 zero-order Legendre 多项式
>>> eval_legendre(0, 0) 1.0计算 -1 和 1 之间的 first-order Legendre 多项式
>>> X = np.linspace(-1, 1, 5) # Domain of Legendre polynomials >>> eval_legendre(1, X) array([-1. , -0.5, 0. , 0.5, 1. ])在 x = 0 处计算 0 到 4 阶的勒让德多项式
>>> N = range(0, 5) >>> eval_legendre(N, 0) array([ 1. , 0. , -0.5 , 0. , 0.375])绘制 0 到 4 阶的勒让德多项式
>>> X = np.linspace(-1, 1)>>> import matplotlib.pyplot as plt >>> for n in range(0, 5): ... y = eval_legendre(n, X) ... plt.plot(X, y, label=r'$P_{}(x)$'.format(n))>>> plt.title("Legendre Polynomials") >>> plt.xlabel("x") >>> plt.ylabel(r'$P_n(x)$') >>> plt.legend(loc='lower right') >>> plt.show()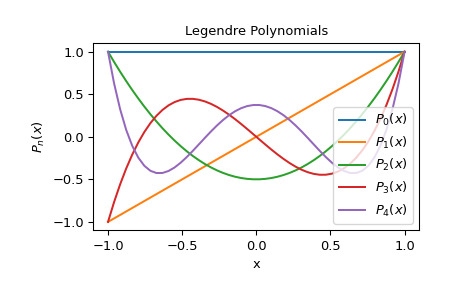
相关用法
- Python SciPy special.eval_chebyc用法及代码示例
- Python SciPy special.eval_chebys用法及代码示例
- Python SciPy special.exp1用法及代码示例
- Python SciPy special.expn用法及代码示例
- Python SciPy special.ellip_harm_2用法及代码示例
- Python SciPy special.expit用法及代码示例
- Python SciPy special.expm1用法及代码示例
- Python SciPy special.ellip_normal用法及代码示例
- Python SciPy special.erfinv用法及代码示例
- Python SciPy special.erf用法及代码示例
- Python SciPy special.ellipj用法及代码示例
- Python SciPy special.erf_zeros用法及代码示例
- Python SciPy special.erfi用法及代码示例
- Python SciPy special.erfc用法及代码示例
- Python SciPy special.erfcx用法及代码示例
- Python SciPy special.expi用法及代码示例
- Python SciPy special.ellipe用法及代码示例
- Python SciPy special.exp10用法及代码示例
- Python SciPy special.exp2用法及代码示例
- Python SciPy special.erfcinv用法及代码示例
- Python SciPy special.elliprd用法及代码示例
- Python SciPy special.exprel用法及代码示例
- Python SciPy special.euler用法及代码示例
- Python SciPy special.errstate用法及代码示例
- Python SciPy special.ellip_harm用法及代码示例
注:本文由纯净天空筛选整理自scipy.org大神的英文原创作品 scipy.special.eval_legendre。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
