本文簡要介紹 python 語言中 scipy.interpolate.UnivariateSpline 的用法。
用法:
class scipy.interpolate.UnivariateSpline(x, y, w=None, bbox=[None, None], k=3, s=None, ext=0, check_finite=False)#一維平滑樣條擬合到一組給定的數據點。
將 k 次的樣條 y = spl(x) 擬合到提供的 x, y 數據。 s 通過指定平滑條件來指定節數。
- x: (N,) 數組
獨立輸入數據的一維數組。必須增加;如果 s 為 0,則必須嚴格遞增。
- y: (N,) 數組
與 x 長度相同的相關輸入數據的一維數組。
- w: (N,) 數組, 可選
樣條擬合的權重。必須是正的。如果w為None,則權重均為1。默認為None。
- bbox: (2,) 類數組,可選
2-sequence 指定近似區間的邊界。如果盒子是無,
bbox=[x[0], x[-1]].默認為無。- k: 整數,可選
平滑樣條的度數。必須是 1 <=k<= 5。
k = 3是三次樣條。默認值為 3。- s: 浮點數或無,可選
用於選擇結數的正平滑因子。節點數將增加,直到滿足平滑條件:
sum((w[i] * (y[i]-spl(x[i])))**2, axis=0) <= s但由於數值問題,實際情況是:
abs(sum((w[i] * (y[i]-spl(x[i])))**2, axis=0) - s) < 0.001 * s如果s是無,s將被設置為長度(寬)用於使用所有數據點的平滑樣條。如果為 0,樣條曲線將通過所有數據點進行插值。這相當於scipy.interpolate.InterpolatedUnivariateSpline。默認為“無”。用戶可以使用s控製貼合的緊密度和平滑度之間的權衡。較大s意味著更平滑,而較小的值s表示平滑度較低。的推薦值s取決於權重,w。如果權重代表標準差的倒數y,那麽一個好的s值應在 (m-sqrt(2*m),m+sqrt(2*m)) 範圍內找到,其中 m 是數據點的數量x,y, 和w。這意味著
s = len(w)應該是一個很好的值,如果1/w[i]是標準差的估計值y[i].- ext: int 或 str,可選
控製不在節點序列定義的區間內的元素的外推模式。
如果 ext=0 或 ‘extrapolate’,則返回外推值。
如果 ext=1 或 ‘zeros’,返回 0
如果 ext=2 或‘raise’,則引發ValueError
如果 ext=3 或‘const’,則返回邊界值。
默認值為 0。
- check_finite: 布爾型,可選
是否檢查輸入數組是否僅包含有限數。禁用可能會提高性能,但如果輸入確實包含無窮大或 NaN,則可能會導致問題(崩潰、非終止或無意義的結果)。默認為假。
參數 ::
注意:
數據點的數量必須大於樣條度 k。
NaN 處理:如果輸入數組包含
nan值,結果沒有用,因為底層的樣條擬合例程無法處理nan.一種解決方法是對not-a-number 數據點使用零權重:>>> import numpy as np >>> from scipy.interpolate import UnivariateSpline >>> x, y = np.array([1, 2, 3, 4]), np.array([1, np.nan, 3, 4]) >>> w = np.isnan(y) >>> y[w] = 0. >>> spl = UnivariateSpline(x, y, w=~w)請注意,需要用數值替換
nan(隻要相應的權重為零,精確值無關緊要。)參考:
基於 [1]、[2]、[3] 和 [4] 中說明的算法:
[1]P. Dierckx,“使用樣條函數對實驗數據進行平滑、微分和積分的算法”,J.Comp.Appl.Maths 1 (1975) 165-184。
[2]P. Dierckx,“使用樣條函數在矩形網格上平滑數據的快速算法”,SIAM J.Numer.Anal。 19 (1982) 1286-1304。
[3]P. Dierckx,“用樣條函數進行曲線擬合的改進算法”,報告 tw54,計算機科學係,K.U.魯汶,1981 年。
[4]P. Dierckx,“用樣條擬合曲線和曲麵”,數值分析專著,牛津大學出版社,1993 年。
例子:
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy.interpolate import UnivariateSpline >>> rng = np.random.default_rng() >>> x = np.linspace(-3, 3, 50) >>> y = np.exp(-x**2) + 0.1 * rng.standard_normal(50) >>> plt.plot(x, y, 'ro', ms=5)使用平滑參數的默認值:
>>> spl = UnivariateSpline(x, y) >>> xs = np.linspace(-3, 3, 1000) >>> plt.plot(xs, spl(xs), 'g', lw=3)手動更改平滑量:
>>> spl.set_smoothing_factor(0.5) >>> plt.plot(xs, spl(xs), 'b', lw=3) >>> plt.show()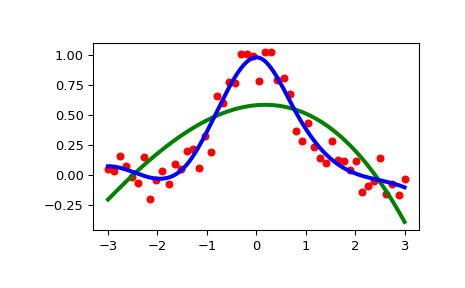
相關用法
- Python SciPy interpolate.make_interp_spline用法及代碼示例
- Python SciPy interpolate.krogh_interpolate用法及代碼示例
- Python SciPy interpolate.InterpolatedUnivariateSpline用法及代碼示例
- Python SciPy interpolate.BSpline用法及代碼示例
- Python SciPy interpolate.LSQSphereBivariateSpline用法及代碼示例
- Python SciPy interpolate.griddata用法及代碼示例
- Python SciPy interpolate.splder用法及代碼示例
- Python SciPy interpolate.LinearNDInterpolator用法及代碼示例
- Python SciPy interpolate.PPoly用法及代碼示例
- Python SciPy interpolate.NdBSpline用法及代碼示例
- Python SciPy interpolate.pade用法及代碼示例
- Python SciPy interpolate.barycentric_interpolate用法及代碼示例
- Python SciPy interpolate.RegularGridInterpolator用法及代碼示例
- Python SciPy interpolate.NdPPoly用法及代碼示例
- Python SciPy interpolate.interp2d用法及代碼示例
- Python SciPy interpolate.approximate_taylor_polynomial用法及代碼示例
- Python SciPy interpolate.RectSphereBivariateSpline用法及代碼示例
- Python SciPy interpolate.sproot用法及代碼示例
- Python SciPy interpolate.splantider用法及代碼示例
- Python SciPy interpolate.CloughTocher2DInterpolator用法及代碼示例
- Python SciPy interpolate.interp1d用法及代碼示例
- Python SciPy interpolate.BPoly用法及代碼示例
- Python SciPy interpolate.BarycentricInterpolator用法及代碼示例
- Python SciPy interpolate.splrep用法及代碼示例
- Python SciPy interpolate.make_smoothing_spline用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.interpolate.UnivariateSpline。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
