Python SciPy interpolate.RegularGridInterpolator用法及代碼示例

本文簡要介紹 python 語言中 scipy.interpolate.RegularGridInterpolator 的用法。

用法:

class  scipy.interpolate.RegularGridInterpolator(points, values, method='linear', bounds_error=True, fill_value=nan)#

在任意維度的規則或直線網格上進行插值。

數據必須在直線網格上定義；即間距均勻或不均勻的矩形網格。支持線性、nearest-neighbor、樣條插值。設置插值器對象後，可以在每次評估時選擇插值方法。

參數 ：：

points： float 的 ndarray 元組，形狀為 (m1, ), ..., (mn, )

定義 n 維規則網格的點。每個維度中的點(即點元組的每個元素)必須嚴格升序或降序。

values： 數組, 形狀 (m1, ..., mn, ...)

n 維規則網格上的數據。複雜的數據是可以接受的。

method： str，可選

要執行的插值方法。支持“linear”, “nearest”, “slinear”, “cubic”, “quintic” 和“pchip”。該參數將成為對象__call__方法的默認參數。默認為“linear”。

bounds_error： 布爾型，可選

如果為 True，則當在輸入數據域之外請求內插值時，會引發 ValueError。如果為 False，則使用fill_value。默認為 True。

fill_value： 浮點數或無，可選

用於插值域之外的點的值。如果沒有，則推斷域外的值。默認為 np.nan 。

注意：

與 LinearNDInterpolator 和 NearestNDInterpolator 相反，此類通過利用規則網格結構避免了昂貴的輸入數據三角測量。

換句話說，此類假設數據是在直線網格上定義的。

‘slinear’(k=1)、‘cubic’(k=3) 和 ‘quintic’(k=5) 方法是 tensor-product 樣條插值器，其中 k 是樣條次數，如果任何維度的點數少於k + 1，將會出現錯誤。

如果輸入數據的維度具有不相稱的單位並且相差多個數量級，則插值可能會出現數值偽影。考慮在插值之前重新縮放數據。

參考：

[1]

Python包規則網格作者：約翰內斯·布赫納 (Johannes Buchner)，參見https://pypi.python.org/pypi/regulargrid/

[2]

維基百科，“Trilinear interpolation”，https://en.wikipedia.org/wiki/Trilinear_interpolation

[3]

韋瑟、艾倫和塞爾吉奧·E·紮蘭托內洛。 “關於多維度分段線性和多線性表插值的注釋。”數學。計算。 50.181(1988)：189-196。https://www.ams.org/journals/mcom/1988-50-181/S0025-5718-1988-0917826-0/S0025-5718-1988-0917826-0.pdf DOI:10.1090/S0025-5718-1988-0917826-0

例子：

評估 3D 網格點上的函數

作為第一個示例，我們在 3D 網格的點上評估一個簡單的示例函數：

>>> from scipy.interpolate import RegularGridInterpolator
>>> import numpy as np
>>> def f(x, y, z):
...     return 2 * x**3 + 3 * y**2 - z
>>> x = np.linspace(1, 4, 11)
>>> y = np.linspace(4, 7, 22)
>>> z = np.linspace(7, 9, 33)
>>> xg, yg ,zg = np.meshgrid(x, y, z, indexing='ij', sparse=True)
>>> data = f(xg, yg, zg)

data 現在是帶有 data[i, j, k] = f(x[i], y[j], z[k]) 的 3-D 數組。接下來，根據這些數據定義一個插值函數：

>>> interp = RegularGridInterpolator((x, y, z), data)

在 (x,y,z) = (2.1, 6.2, 8.3) 和 (3.3, 5.2, 7.1) 兩點評估插值函數：

>>> pts = np.array([[2.1, 6.2, 8.3],
...                 [3.3, 5.2, 7.1]])
>>> interp(pts)
array([ 125.80469388,  146.30069388])

這確實非常接近於

>>> f(2.1, 6.2, 8.3), f(3.3, 5.2, 7.1)
(125.54200000000002, 145.894)

對 2D 數據集進行插值和外推

作為第二個示例，我們對二維數據集進行插值和外推：

>>> x, y = np.array([-2, 0, 4]), np.array([-2, 0, 2, 5])
>>> def ff(x, y):
...     return x**2 + y**2

>>> xg, yg = np.meshgrid(x, y, indexing='ij')
>>> data = ff(xg, yg)
>>> interp = RegularGridInterpolator((x, y), data,
...                                  bounds_error=False, fill_value=None)

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax = fig.add_subplot(projection='3d')
>>> ax.scatter(xg.ravel(), yg.ravel(), data.ravel(),
...            s=60, c='k', label='data')

在更精細的網格上評估和繪製插值器

>>> xx = np.linspace(-4, 9, 31)
>>> yy = np.linspace(-4, 9, 31)
>>> X, Y = np.meshgrid(xx, yy, indexing='ij')

>>> # interpolator
>>> ax.plot_wireframe(X, Y, interp((X, Y)), rstride=3, cstride=3,
...                   alpha=0.4, color='m', label='linear interp')

>>> # ground truth
>>> ax.plot_wireframe(X, Y, ff(X, Y), rstride=3, cstride=3,
...                   alpha=0.4, label='ground truth')
>>> plt.legend()
>>> plt.show()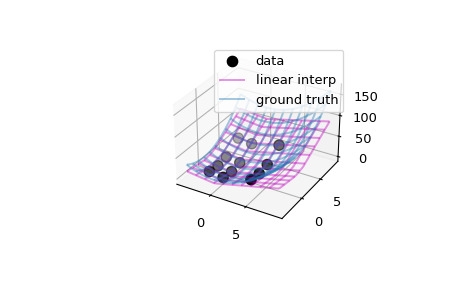

本教程中給出了其他示例。

屬性 ：：

grid： ndarray 的元組

定義 n 維規則網格的點。該元組通過np.meshgrid(*grid, indexing='ij')定義完整網格

values： ndarray

網格上的數據值。

method： str

插值法。

fill_value： 浮點數或None

將此值用於 __call__ 的越界參數。

bounds_error： bool

如果 True ，越界參數引發 ValueError 。