本文簡要介紹 python 語言中 scipy.interpolate.CloughTocher2DInterpolator 的用法。
用法:
class scipy.interpolate.CloughTocher2DInterpolator(points, values, fill_value=nan, tol=1e-06, maxiter=400, rescale=False)#CloughTocher2DInterpolator(點,值,tol=1e-6)。
分段三次,C1 平滑,curvature-minimizing 二維插值。
- points: ndarray 浮點數,形狀(npoints,ndims);或德勞內
數據點坐標的二維數組,或預先計算的 Delaunay 三角剖分。
- values: 浮點數或複數的ndarray,形狀(npoints,...)
N-D 點數據值數組。沿第一個軸的值的長度必須等於點的長度。與某些插補器不同,插補軸無法更改。
- fill_value: 浮點數,可選
用於填充輸入點凸包之外的請求點的值。如果未提供,則默認值為
nan。- tol: 浮點數,可選
梯度估計的絕對/相對容差。
- maxiter: 整數,可選
梯度估計中的最大迭代次數。
- rescale: 布爾型,可選
在執行插值之前將點重新縮放到單位立方體。如果某些輸入維度具有不可比較的單位並且相差許多數量級,這將很有用。
參數 ::
注意:
插值是通過使用 Qhull [1] 對輸入數據進行三角剖分來構造的,並使用 Clough-Tocher 方案 [CT] 在每個三角形上構造分段三次插值 Bezier 多項式。保證插值是連續可微的。
選擇插值的梯度,使得插值表麵的曲率近似最小化。使用 [Nielson83] 和 [Renka84] 中說明的全局算法估計為此所需的梯度。
注意
對於常規網格上的數據,請改用
interpn。參考:
[CT]例如,參見 P. Alfeld,“用於四麵體數據的三變量 Clough-Tocher 方案”。計算機輔助幾何設計,1, 169 (1984); G. Farin,“三角形Bernstein-Bezier 補丁”。計算機輔助幾何設計,3, 83 (1986)。
[尼爾森83]G. Nielson,“基於最小範數網絡內插分散數據的方法”。數學。比較,40, 253 (1983)。
[仁卡84]R. J. Renka 和 A. K. Cline。 “基於三角形的 C1 插值方法。”,落基山 J. Math., 14, 223 (1984)。
例子:
我們可以在 2D 平麵上插值:
>>> from scipy.interpolate import CloughTocher2DInterpolator >>> import numpy as np >>> import matplotlib.pyplot as plt >>> rng = np.random.default_rng() >>> x = rng.random(10) - 0.5 >>> y = rng.random(10) - 0.5 >>> z = np.hypot(x, y) >>> X = np.linspace(min(x), max(x)) >>> Y = np.linspace(min(y), max(y)) >>> X, Y = np.meshgrid(X, Y) # 2D grid for interpolation >>> interp = CloughTocher2DInterpolator(list(zip(x, y)), z) >>> Z = interp(X, Y) >>> plt.pcolormesh(X, Y, Z, shading='auto') >>> plt.plot(x, y, "ok", label="input point") >>> plt.legend() >>> plt.colorbar() >>> plt.axis("equal") >>> plt.show()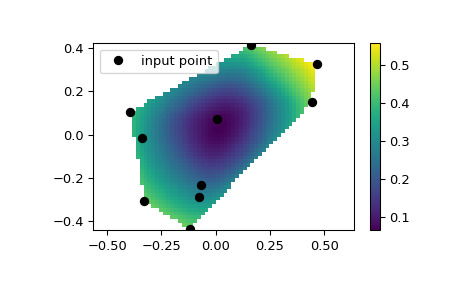
相關用法
- Python SciPy interpolate.CubicSpline用法及代碼示例
- Python SciPy interpolate.make_interp_spline用法及代碼示例
- Python SciPy interpolate.krogh_interpolate用法及代碼示例
- Python SciPy interpolate.InterpolatedUnivariateSpline用法及代碼示例
- Python SciPy interpolate.BSpline用法及代碼示例
- Python SciPy interpolate.LSQSphereBivariateSpline用法及代碼示例
- Python SciPy interpolate.griddata用法及代碼示例
- Python SciPy interpolate.splder用法及代碼示例
- Python SciPy interpolate.LinearNDInterpolator用法及代碼示例
- Python SciPy interpolate.PPoly用法及代碼示例
- Python SciPy interpolate.NdBSpline用法及代碼示例
- Python SciPy interpolate.pade用法及代碼示例
- Python SciPy interpolate.barycentric_interpolate用法及代碼示例
- Python SciPy interpolate.RegularGridInterpolator用法及代碼示例
- Python SciPy interpolate.NdPPoly用法及代碼示例
- Python SciPy interpolate.interp2d用法及代碼示例
- Python SciPy interpolate.approximate_taylor_polynomial用法及代碼示例
- Python SciPy interpolate.RectSphereBivariateSpline用法及代碼示例
- Python SciPy interpolate.sproot用法及代碼示例
- Python SciPy interpolate.splantider用法及代碼示例
- Python SciPy interpolate.interp1d用法及代碼示例
- Python SciPy interpolate.BPoly用法及代碼示例
- Python SciPy interpolate.BarycentricInterpolator用法及代碼示例
- Python SciPy interpolate.splrep用法及代碼示例
- Python SciPy interpolate.make_smoothing_spline用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.interpolate.CloughTocher2DInterpolator。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
