本文簡要介紹 python 語言中 scipy.interpolate.RectSphereBivariateSpline 的用法。
用法:
class scipy.interpolate.RectSphereBivariateSpline(u, v, r, s=0.0, pole_continuity=False, pole_values=None, pole_exact=False, pole_flat=False)#球體上矩形網格上的二元樣條近似。
可用於平滑數據。
- u: array_like
嚴格按升序排列的一維緯度坐標數組。坐標必須以弧度表示並且位於開放區間
(0, pi)內。- v: array_like
嚴格按升序排列的一維經度坐標數組。坐標必須以弧度表示。第一個元素 (
v[0]) 必須位於區間[-pi, pi)內。最後一個元素 (v[-1]) 必須滿足v[-1] <= v[0] + 2*pi。- r: array_like
形狀為
(u.size, v.size)的二維數據數組。- s: 浮點數,可選
為估計條件定義的正平滑因子(
s=0用於插值)。- pole_continuity: bool or (bool, bool), 可選
u=0(pole_continuity[0]) 和u=pi(pole_continuity[1]) 兩極的連續性順序。當它為真或假時,極點的連續性順序將分別為 1 或 0。默認為假。- pole_values: 浮點數或(浮點數,浮點數),可選
極點
u=0和u=pi的數據值。整個參數或每個單獨的元素都可以是 None。默認為無。- pole_exact: bool or (bool, bool), 可選
極點
u=0和u=pi的數據值準確性。如果為 True,則該值被認為是正確的函數值,它將被精確擬合。如果為 False,則該值將被視為與其他數據值一樣的數據值。默認為假。- pole_flat: bool or (bool, bool), 可選
對於
u=0和u=pi處的極點,指定近似值是否具有消失導數。默認為假。
參數 ::
注意:
目前,僅支持平滑樣條近似(FITPACK 例程中的
iopt[0] = 0和iopt[0] = 1)。精確的最小二乘樣條近似尚未實現。在實際執行插值時,請求的 v 值必須位於與選擇原始 v 值相同的長度 2pi 間隔內。
有關詳細信息,請參閱有關此函數的FITPACK 站點。
例子:
假設我們在粗網格上有全局數據
>>> import numpy as np >>> lats = np.linspace(10, 170, 9) * np.pi / 180. >>> lons = np.linspace(0, 350, 18) * np.pi / 180. >>> data = np.dot(np.atleast_2d(90. - np.linspace(-80., 80., 18)).T, ... np.atleast_2d(180. - np.abs(np.linspace(0., 350., 9)))).T我們想將其插入到全局one-degree 網格中
>>> new_lats = np.linspace(1, 180, 180) * np.pi / 180 >>> new_lons = np.linspace(1, 360, 360) * np.pi / 180 >>> new_lats, new_lons = np.meshgrid(new_lats, new_lons)我們需要設置插值器對象
>>> from scipy.interpolate import RectSphereBivariateSpline >>> lut = RectSphereBivariateSpline(lats, lons, data)最後我們對數據進行插值。
RectSphereBivariateSpline對象僅接受一維數組作為輸入,因此我們需要進行一些重塑。>>> data_interp = lut.ev(new_lats.ravel(), ... new_lons.ravel()).reshape((360, 180)).T查看原始數據和插值後的數據,可以看到插值法很好地再現了原始數據:
>>> import matplotlib.pyplot as plt >>> fig = plt.figure() >>> ax1 = fig.add_subplot(211) >>> ax1.imshow(data, interpolation='nearest') >>> ax2 = fig.add_subplot(212) >>> ax2.imshow(data_interp, interpolation='nearest') >>> plt.show()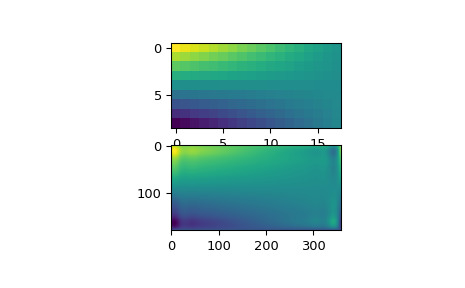
選擇
s的最佳值可能是一項艱巨的任務。s的推薦值取決於數據值的準確性。如果用戶對數據的統計誤差有所了解,她還可以找到s的正確估計值。通過假設,如果她指定正確的s,則插值器將使用樣條f(u,v)精確再現數據基礎的函數,她可以評估sum((r(i,j)-s(u(i),v(j)))**2)以找到對此s的良好估計。例如,如果她知道她的r(i,j)值上的統計誤差不大於 0.1,她可能會期望一個好的s的值應該不大於u.size * v.size * (0.1)**2。如果對
r(i,j)中的統計錯誤一無所知,則必須通過反複試驗來確定s。最好的方法是從s的非常大的值開始(以確定最小二乘多項式和s的相應上限fp0),然後逐漸減小s的值(例如開始時因子 10,即s = fp0 / 10, fp0 / 100, ...,並且更仔細,因為近似值顯示更多細節)以獲得更接近的擬合。s的不同值的插值結果可以深入了解這個過程:>>> fig2 = plt.figure() >>> s = [3e9, 2e9, 1e9, 1e8] >>> for idx, sval in enumerate(s, 1): ... lut = RectSphereBivariateSpline(lats, lons, data, s=sval) ... data_interp = lut.ev(new_lats.ravel(), ... new_lons.ravel()).reshape((360, 180)).T ... ax = fig2.add_subplot(2, 2, idx) ... ax.imshow(data_interp, interpolation='nearest') ... ax.set_title(f"s = {sval:g}") >>> plt.show()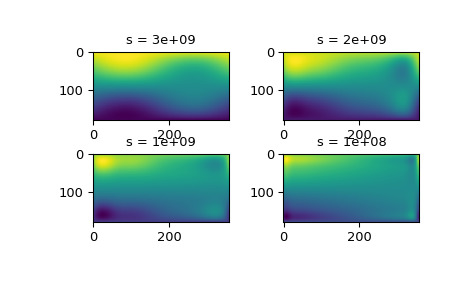
相關用法
- Python SciPy interpolate.RegularGridInterpolator用法及代碼示例
- Python SciPy interpolate.Rbf用法及代碼示例
- Python SciPy interpolate.RBFInterpolator用法及代碼示例
- Python SciPy interpolate.make_interp_spline用法及代碼示例
- Python SciPy interpolate.krogh_interpolate用法及代碼示例
- Python SciPy interpolate.InterpolatedUnivariateSpline用法及代碼示例
- Python SciPy interpolate.BSpline用法及代碼示例
- Python SciPy interpolate.LSQSphereBivariateSpline用法及代碼示例
- Python SciPy interpolate.griddata用法及代碼示例
- Python SciPy interpolate.splder用法及代碼示例
- Python SciPy interpolate.LinearNDInterpolator用法及代碼示例
- Python SciPy interpolate.PPoly用法及代碼示例
- Python SciPy interpolate.NdBSpline用法及代碼示例
- Python SciPy interpolate.pade用法及代碼示例
- Python SciPy interpolate.barycentric_interpolate用法及代碼示例
- Python SciPy interpolate.NdPPoly用法及代碼示例
- Python SciPy interpolate.interp2d用法及代碼示例
- Python SciPy interpolate.approximate_taylor_polynomial用法及代碼示例
- Python SciPy interpolate.sproot用法及代碼示例
- Python SciPy interpolate.splantider用法及代碼示例
- Python SciPy interpolate.CloughTocher2DInterpolator用法及代碼示例
- Python SciPy interpolate.interp1d用法及代碼示例
- Python SciPy interpolate.BPoly用法及代碼示例
- Python SciPy interpolate.BarycentricInterpolator用法及代碼示例
- Python SciPy interpolate.splrep用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.interpolate.RectSphereBivariateSpline。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
