本文简要介绍 python 语言中 scipy.signal.lombscargle 的用法。
用法:
scipy.signal.lombscargle(x, y, freqs)#计算Lomb-Scargle 周期图。
Lomb-Scargle 周期图由 Lomb [1] 开发,并由 Scargle [2] 进一步扩展,以发现和测试时间采样不均匀的弱周期信号的重要性。
什么时候标准化为 False (默认) 计算的周期图未归一化,它取值
(A**2) * N/4对于振幅为 A 的谐波信号,N 足够大。当 normalize 为 True 时,计算的周期图由围绕恒定参考模型(为零)的数据残差进行归一化。
输入数组应该是一维的并且将被强制转换为 float64。
- x: array_like
采样时间。
- y: array_like
测量值。
- freqs: array_like
输出周期图的角频率。
- precenter: 布尔型,可选
通过减去平均值预中心测量值。
- normalize: 布尔型,可选
计算归一化周期图。
- pgram: array_like
Lomb-Scargle 周期图。
- ValueError
如果输入数组 x 和 y 的形状不同。
参数 ::
返回 ::
抛出 ::
注意:
由于 Townsend [3],该子例程使用稍微修改的算法计算周期图,该算法允许对每个频率仅使用一次通过输入数组来计算周期图。
对于大量样本和频率,算法运行时间大致为 O(x * freqs) 或 O(N^2)。
参考:
[1]N.R. Lomb“不等距数据的最小二乘频率分析”,天体物理学和空间科学,第 39 卷,第 447-462 页,1976 年
[2]J.D. Scargle“天文时间序列分析研究。 II - 不均匀间隔数据的频谱分析的统计方面”,《天体物理学杂志》,第 263 卷,第 835-853 页,1982 年
[3]R.H.D. Townsend,“使用图形处理单元快速计算Lomb-Scargle 周期图。”,天体物理学杂志增刊系列,第 191 卷,第 247-253 页,2010
例子:
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> rng = np.random.default_rng()首先为信号定义一些输入参数:
>>> A = 2. >>> w0 = 1. # rad/sec >>> nin = 150 >>> nout = 100000随机生成采样时间:
>>> x = rng.uniform(0, 10*np.pi, nin)绘制选定时间的正弦波:
>>> y = A * np.cos(w0*x)定义要计算周期图的频率数组:
>>> w = np.linspace(0.01, 10, nout)计算Lomb-Scargle 周期图:
>>> import scipy.signal as signal >>> pgram = signal.lombscargle(x, y, w, normalize=True)现在绘制输入数据图:
>>> fig, (ax_t, ax_w) = plt.subplots(2, 1, constrained_layout=True) >>> ax_t.plot(x, y, 'b+') >>> ax_t.set_xlabel('Time [s]')然后绘制归一化周期图:
>>> ax_w.plot(w, pgram) >>> ax_w.set_xlabel('Angular frequency [rad/s]') >>> ax_w.set_ylabel('Normalized amplitude') >>> plt.show()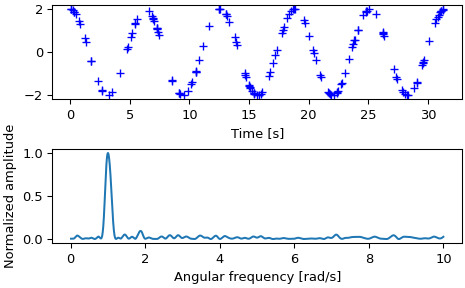
相关用法
- Python SciPy signal.lfilter用法及代码示例
- Python SciPy signal.lfilter_zi用法及代码示例
- Python SciPy signal.lp2hp用法及代码示例
- Python SciPy signal.lti用法及代码示例
- Python SciPy signal.lp2bs_zpk用法及代码示例
- Python SciPy signal.lp2bp_zpk用法及代码示例
- Python SciPy signal.lsim用法及代码示例
- Python SciPy signal.lp2bs用法及代码示例
- Python SciPy signal.lp2bp用法及代码示例
- Python SciPy signal.lp2hp_zpk用法及代码示例
- Python SciPy signal.lsim2用法及代码示例
- Python SciPy signal.lp2lp_zpk用法及代码示例
- Python SciPy signal.lp2lp用法及代码示例
- Python SciPy signal.czt_points用法及代码示例
- Python SciPy signal.chirp用法及代码示例
- Python SciPy signal.residue用法及代码示例
- Python SciPy signal.iirdesign用法及代码示例
- Python SciPy signal.max_len_seq用法及代码示例
- Python SciPy signal.kaiser_atten用法及代码示例
- Python SciPy signal.oaconvolve用法及代码示例
- Python SciPy signal.hilbert用法及代码示例
- Python SciPy signal.ricker用法及代码示例
- Python SciPy signal.group_delay用法及代码示例
- Python SciPy signal.cheb2ord用法及代码示例
- Python SciPy signal.get_window用法及代码示例
注:本文由纯净天空筛选整理自scipy.org大神的英文原创作品 scipy.signal.lombscargle。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
