本文简要介绍 python 语言中 scipy.signal.chirp 的用法。
用法:
scipy.signal.chirp(t, f0, t1, f1, method='linear', phi=0, vertex_zero=True)#Frequency-swept 余弦发生器。
在下文中,“Hz”应解释为“每单位的周期数”;这里没有要求单位是一秒。重要的区别是旋转单位是周期,而不是弧度。同样,t 可以是空间而不是时间的度量。
- t: array_like
评估波形的时间。
- f0: 浮点数
时间 t=0 时的频率(例如 Hz)。
- t1: 浮点数
指定 f1 的时间。
- f1: 浮点数
时间 t1 处波形的频率(例如 Hz)。
- method: {‘linear’, ‘quadratic’, ‘logarithmic’, ‘hyperbolic’},可选
一种频率扫描。如果未给出,则假定为线性。有关详细信息,请参阅下面的注释。
- phi: 浮点数,可选
相位偏移,以度为单位。默认值为 0。
- vertex_zero: 布尔型,可选
此参数仅在方法为‘quadratic’ 时使用。它确定作为频率图的抛物线的顶点是在t=0还是t=t1。
- y: ndarray
一个 numpy 数组,其中包含在t与请求的time-varying 频率。更准确地说,函数返回
cos(phase + (pi/180)*phi)其中阶段是积分(从 0 到t) 的2*pi*f(t).f(t)定义如下。
参数 ::
返回 ::
注意:
该方法有四个选项。以下公式给出了chirp() 生成的信号的瞬时频率(以赫兹为单位)。为方便起见,也可以使用下面显示的较短名称。
linear, lin, li:
f(t) = f0 + (f1 - f0) * t / t1二次,四边形,q:
The graph of the frequency f(t) is a parabola through (0, f0) and (t1, f1). By default, the vertex of the parabola is at (0, f0). If vertex_zero is False, then the vertex is at (t1, f1). The formula is:
if vertex_zero is True:
f(t) = f0 + (f1 - f0) * t**2 / t1**2else:
f(t) = f1 - (f1 - f0) * (t1 - t)**2 / t1**2To use a more general quadratic function, or an arbitrary polynomial, use the function
scipy.signal.sweep_poly.对数,log,lo:
f(t) = f0 * (f1/f0)**(t/t1)f0 and f1 must be nonzero and have the same sign.
This signal is also known as a geometric or exponential chirp.
双曲线,炒作:
f(t) = f0*f1*t1 / ((f0 - f1)*t + f1*t1)f0 and f1 must be nonzero.
例子:
示例中将使用以下内容:
>>> import numpy as np >>> from scipy.signal import chirp, spectrogram >>> import matplotlib.pyplot as plt对于第一个示例,我们将绘制 10 秒内从 6 Hz 到 1 Hz 的线性啁啾的波形:
>>> t = np.linspace(0, 10, 1500) >>> w = chirp(t, f0=6, f1=1, t1=10, method='linear') >>> plt.plot(t, w) >>> plt.title("Linear Chirp, f(0)=6, f(10)=1") >>> plt.xlabel('t (sec)') >>> plt.show()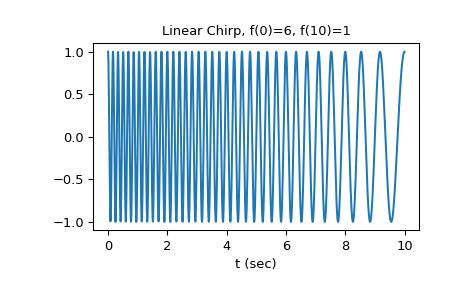
对于其余示例,我们将使用更高的频率范围,并使用
scipy.signal.spectrogram演示结果。我们将使用以 7200 Hz 采样的 4 秒间隔。>>> fs = 7200 >>> T = 4 >>> t = np.arange(0, int(T*fs)) / fs我们将使用这个函数来绘制每个示例中的频谱图。
>>> def plot_spectrogram(title, w, fs): ... ff, tt, Sxx = spectrogram(w, fs=fs, nperseg=256, nfft=576) ... fig, ax = plt.subplots() ... ax.pcolormesh(tt, ff[:145], Sxx[:145], cmap='gray_r', ... shading='gouraud') ... ax.set_title(title) ... ax.set_xlabel('t (sec)') ... ax.set_ylabel('Frequency (Hz)') ... ax.grid(True) ...从 1500 Hz 到 250 Hz 的二次啁啾(频率抛物线的顶点在 t=0):
>>> w = chirp(t, f0=1500, f1=250, t1=T, method='quadratic') >>> plot_spectrogram(f'Quadratic Chirp, f(0)=1500, f({T})=250', w, fs) >>> plt.show()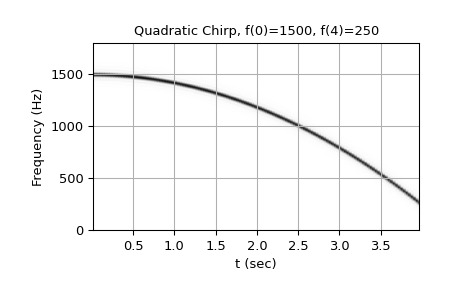
从 1500 Hz 到 250 Hz 的二次啁啾(频率抛物线的顶点在 t=T):
>>> w = chirp(t, f0=1500, f1=250, t1=T, method='quadratic', ... vertex_zero=False) >>> plot_spectrogram(f'Quadratic Chirp, f(0)=1500, f({T})=250\n' + ... '(vertex_zero=False)', w, fs) >>> plt.show()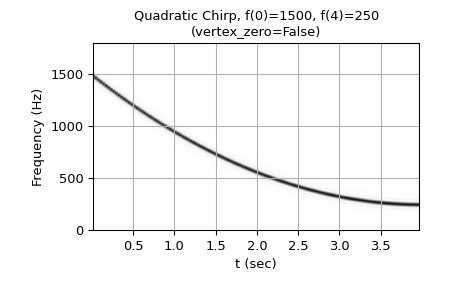
从 1500 Hz 到 250 Hz 的对数啁啾:
>>> w = chirp(t, f0=1500, f1=250, t1=T, method='logarithmic') >>> plot_spectrogram(f'Logarithmic Chirp, f(0)=1500, f({T})=250', w, fs) >>> plt.show()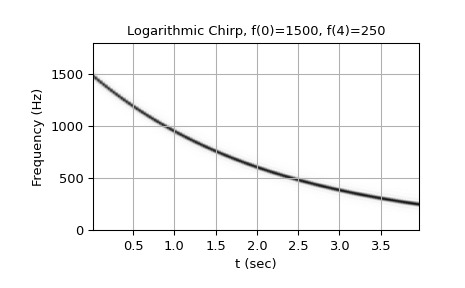
从 1500 Hz 到 250 Hz 的双曲线啁啾:
>>> w = chirp(t, f0=1500, f1=250, t1=T, method='hyperbolic') >>> plot_spectrogram(f'Hyperbolic Chirp, f(0)=1500, f({T})=250', w, fs) >>> plt.show()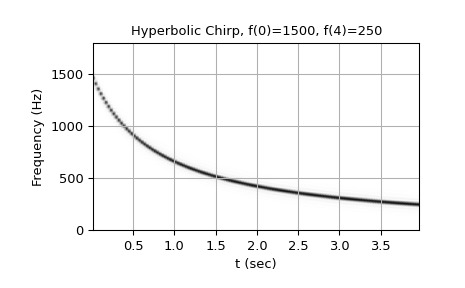
相关用法
- Python SciPy signal.cheb2ord用法及代码示例
- Python SciPy signal.cheb1ord用法及代码示例
- Python SciPy signal.cheby2用法及代码示例
- Python SciPy signal.cheby1用法及代码示例
- Python SciPy signal.check_COLA用法及代码示例
- Python SciPy signal.choose_conv_method用法及代码示例
- Python SciPy signal.check_NOLA用法及代码示例
- Python SciPy signal.czt_points用法及代码示例
- Python SciPy signal.coherence用法及代码示例
- Python SciPy signal.csd用法及代码示例
- Python SciPy signal.correlate2d用法及代码示例
- Python SciPy signal.cubic用法及代码示例
- Python SciPy signal.correlation_lags用法及代码示例
- Python SciPy signal.convolve2d用法及代码示例
- Python SciPy signal.cspline1d用法及代码示例
- Python scipy.signal.czt用法及代码示例
- Python SciPy signal.cwt用法及代码示例
- Python SciPy signal.convolve用法及代码示例
- Python SciPy signal.cont2discrete用法及代码示例
- Python SciPy signal.cspline1d_eval用法及代码示例
- Python SciPy signal.cmplx_sort用法及代码示例
- Python SciPy signal.correlate用法及代码示例
- Python SciPy signal.residue用法及代码示例
- Python SciPy signal.iirdesign用法及代码示例
- Python SciPy signal.max_len_seq用法及代码示例
注:本文由纯净天空筛选整理自scipy.org大神的英文原创作品 scipy.signal.chirp。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
