本文简要介绍 python 语言中 scipy.signal.cont2discrete 的用法。
用法:
scipy.signal.cont2discrete(system, dt, method='zoh', alpha=None)#将连续状态空间系统转换为离散状态空间系统。
- system: 说明系统的元组或
lti的实例 下面给出元组中元素的数量和解释:
1: (instance of
lti)2: (num, den)
3: (zeros, poles, gain)
4: (A, B, C, D)
- dt: 浮点数
离散化时间步长。
- method: str,可选
使用哪种方法:
gbt: generalized bilinear transformation
bilinear: Tustin’s approximation (“gbt” with alpha=0.5)
euler: Euler (or forward differencing) method (“gbt” with alpha=0)
backward_diff: Backwards differencing (“gbt” with alpha=1.0)
zoh: zero-order hold (default)
foh: first-order hold (versionadded: 1.3.0)
impulse: equivalent impulse response (versionadded: 1.3.0)
- alpha: 在 [0, 1] 内浮点数,可选
广义双线性变换加权参数,只能用method=”gbt”指定,否则忽略
- system: 说明系统的元组或
- sysd: 包含离散系统的元组
根据输入类型,输出将采用以下形式
(num, den, dt) 用于传递函数输入
zeros-poles-gain 输入的(零点、极点、增益、dt)
(A, B, C, D, dt) 用于状态空间系统输入
参数 ::
返回 ::
注意:
默认情况下,例程使用Zero-Order Hold (zoh) 方法来执行转换。或者,可以使用广义双线性变换,包括常见的 Tustin 双线性近似、欧拉方法技术或反向差分技术。
Zero-OrderHold(zoh)方法基于[1],广义双线性近似基于[2]和[3],First-OrderHold(foh)方法基于[4]。
参考:
[3]G.Zhang、X.Chen 和 T.Chen,通过广义双线性变换进行数字重新设计,Int。 J.控制,卷。 82、没有。 4,第 741-754 页,2009 年。(https://www.mypolyuweb.hk/~magzhang/Research/ZCC09_IJC.pdf)
[4]G. F. Franklin、J. D. Powell 和 M. L. Workman,动态系统的数字控制,第 3 版。加利福尼亚州门洛帕克:Addison-Wesley,第 204-206 页,1998 年。
例子:
我们可以将连续状态空间系统转换为离散状态空间系统:
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy.signal import cont2discrete, lti, dlti, dstep定义连续状态空间系统。
>>> A = np.array([[0, 1],[-10., -3]]) >>> B = np.array([[0],[10.]]) >>> C = np.array([[1., 0]]) >>> D = np.array([[0.]]) >>> l_system = lti(A, B, C, D) >>> t, x = l_system.step(T=np.linspace(0, 5, 100)) >>> fig, ax = plt.subplots() >>> ax.plot(t, x, label='Continuous', linewidth=3)使用多种方法将其转换为离散状态空间系统。
>>> dt = 0.1 >>> for method in ['zoh', 'bilinear', 'euler', 'backward_diff', 'foh', 'impulse']: ... d_system = cont2discrete((A, B, C, D), dt, method=method) ... s, x_d = dstep(d_system) ... ax.step(s, np.squeeze(x_d), label=method, where='post') >>> ax.axis([t[0], t[-1], x[0], 1.4]) >>> ax.legend(loc='best') >>> fig.tight_layout() >>> plt.show()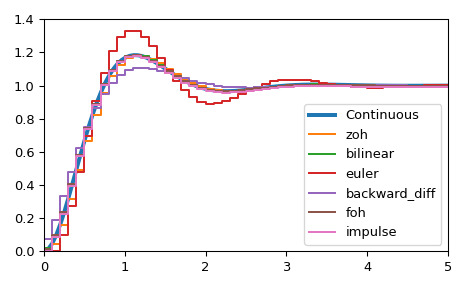
相关用法
- Python SciPy signal.convolve2d用法及代码示例
- Python SciPy signal.convolve用法及代码示例
- Python SciPy signal.coherence用法及代码示例
- Python SciPy signal.correlate2d用法及代码示例
- Python SciPy signal.correlation_lags用法及代码示例
- Python SciPy signal.correlate用法及代码示例
- Python SciPy signal.czt_points用法及代码示例
- Python SciPy signal.chirp用法及代码示例
- Python SciPy signal.cheb2ord用法及代码示例
- Python SciPy signal.cheb1ord用法及代码示例
- Python SciPy signal.csd用法及代码示例
- Python SciPy signal.cubic用法及代码示例
- Python SciPy signal.cheby2用法及代码示例
- Python SciPy signal.cheby1用法及代码示例
- Python SciPy signal.cspline1d用法及代码示例
- Python SciPy signal.check_COLA用法及代码示例
- Python scipy.signal.czt用法及代码示例
- Python SciPy signal.choose_conv_method用法及代码示例
- Python SciPy signal.cwt用法及代码示例
- Python SciPy signal.cspline1d_eval用法及代码示例
- Python SciPy signal.cmplx_sort用法及代码示例
- Python SciPy signal.check_NOLA用法及代码示例
- Python SciPy signal.residue用法及代码示例
- Python SciPy signal.iirdesign用法及代码示例
- Python SciPy signal.max_len_seq用法及代码示例
注:本文由纯净天空筛选整理自scipy.org大神的英文原创作品 scipy.signal.cont2discrete。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
