本文簡要介紹 python 語言中 scipy.signal.cont2discrete 的用法。
用法:
scipy.signal.cont2discrete(system, dt, method='zoh', alpha=None)#將連續狀態空間係統轉換為離散狀態空間係統。
- system: 說明係統的元組或
lti的實例 下麵給出元組中元素的數量和解釋:
1: (instance of
lti)2: (num, den)
3: (zeros, poles, gain)
4: (A, B, C, D)
- dt: 浮點數
離散化時間步長。
- method: str,可選
使用哪種方法:
gbt: generalized bilinear transformation
bilinear: Tustin’s approximation (“gbt” with alpha=0.5)
euler: Euler (or forward differencing) method (“gbt” with alpha=0)
backward_diff: Backwards differencing (“gbt” with alpha=1.0)
zoh: zero-order hold (default)
foh: first-order hold (versionadded: 1.3.0)
impulse: equivalent impulse response (versionadded: 1.3.0)
- alpha: 在 [0, 1] 內浮點數,可選
廣義雙線性變換加權參數,隻能用method=”gbt”指定,否則忽略
- system: 說明係統的元組或
- sysd: 包含離散係統的元組
根據輸入類型,輸出將采用以下形式
(num, den, dt) 用於傳遞函數輸入
zeros-poles-gain 輸入的(零點、極點、增益、dt)
(A, B, C, D, dt) 用於狀態空間係統輸入
參數 ::
返回 ::
注意:
默認情況下,例程使用Zero-Order Hold (zoh) 方法來執行轉換。或者,可以使用廣義雙線性變換,包括常見的 Tustin 雙線性近似、歐拉方法技術或反向差分技術。
Zero-OrderHold(zoh)方法基於[1],廣義雙線性近似基於[2]和[3],First-OrderHold(foh)方法基於[4]。
參考:
[3]G.Zhang、X.Chen 和 T.Chen,通過廣義雙線性變換進行數字重新設計,Int。 J.控製,卷。 82、沒有。 4,第 741-754 頁,2009 年。(https://www.mypolyuweb.hk/~magzhang/Research/ZCC09_IJC.pdf)
[4]G. F. Franklin、J. D. Powell 和 M. L. Workman,動態係統的數字控製,第 3 版。加利福尼亞州門洛帕克:Addison-Wesley,第 204-206 頁,1998 年。
例子:
我們可以將連續狀態空間係統轉換為離散狀態空間係統:
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy.signal import cont2discrete, lti, dlti, dstep定義連續狀態空間係統。
>>> A = np.array([[0, 1],[-10., -3]]) >>> B = np.array([[0],[10.]]) >>> C = np.array([[1., 0]]) >>> D = np.array([[0.]]) >>> l_system = lti(A, B, C, D) >>> t, x = l_system.step(T=np.linspace(0, 5, 100)) >>> fig, ax = plt.subplots() >>> ax.plot(t, x, label='Continuous', linewidth=3)使用多種方法將其轉換為離散狀態空間係統。
>>> dt = 0.1 >>> for method in ['zoh', 'bilinear', 'euler', 'backward_diff', 'foh', 'impulse']: ... d_system = cont2discrete((A, B, C, D), dt, method=method) ... s, x_d = dstep(d_system) ... ax.step(s, np.squeeze(x_d), label=method, where='post') >>> ax.axis([t[0], t[-1], x[0], 1.4]) >>> ax.legend(loc='best') >>> fig.tight_layout() >>> plt.show()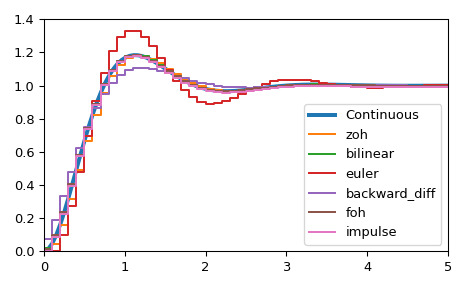
相關用法
- Python SciPy signal.convolve2d用法及代碼示例
- Python SciPy signal.convolve用法及代碼示例
- Python SciPy signal.coherence用法及代碼示例
- Python SciPy signal.correlate2d用法及代碼示例
- Python SciPy signal.correlation_lags用法及代碼示例
- Python SciPy signal.correlate用法及代碼示例
- Python SciPy signal.czt_points用法及代碼示例
- Python SciPy signal.chirp用法及代碼示例
- Python SciPy signal.cheb2ord用法及代碼示例
- Python SciPy signal.cheb1ord用法及代碼示例
- Python SciPy signal.csd用法及代碼示例
- Python SciPy signal.cubic用法及代碼示例
- Python SciPy signal.cheby2用法及代碼示例
- Python SciPy signal.cheby1用法及代碼示例
- Python SciPy signal.cspline1d用法及代碼示例
- Python SciPy signal.check_COLA用法及代碼示例
- Python scipy.signal.czt用法及代碼示例
- Python SciPy signal.choose_conv_method用法及代碼示例
- Python SciPy signal.cwt用法及代碼示例
- Python SciPy signal.cspline1d_eval用法及代碼示例
- Python SciPy signal.cmplx_sort用法及代碼示例
- Python SciPy signal.check_NOLA用法及代碼示例
- Python SciPy signal.residue用法及代碼示例
- Python SciPy signal.iirdesign用法及代碼示例
- Python SciPy signal.max_len_seq用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.signal.cont2discrete。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
