本文簡要介紹 python 語言中 scipy.signal.chirp 的用法。
用法:
scipy.signal.chirp(t, f0, t1, f1, method='linear', phi=0, vertex_zero=True)#Frequency-swept 餘弦發生器。
在下文中,“Hz”應解釋為“每單位的周期數”;這裏沒有要求單位是一秒。重要的區別是旋轉單位是周期,而不是弧度。同樣,t 可以是空間而不是時間的度量。
- t: array_like
評估波形的時間。
- f0: 浮點數
時間 t=0 時的頻率(例如 Hz)。
- t1: 浮點數
指定 f1 的時間。
- f1: 浮點數
時間 t1 處波形的頻率(例如 Hz)。
- method: {‘linear’, ‘quadratic’, ‘logarithmic’, ‘hyperbolic’},可選
一種頻率掃描。如果未給出,則假定為線性。有關詳細信息,請參閱下麵的注釋。
- phi: 浮點數,可選
相位偏移,以度為單位。默認值為 0。
- vertex_zero: 布爾型,可選
此參數僅在方法為‘quadratic’ 時使用。它確定作為頻率圖的拋物線的頂點是在t=0還是t=t1。
- y: ndarray
一個 numpy 數組,其中包含在t與請求的time-varying 頻率。更準確地說,函數返回
cos(phase + (pi/180)*phi)其中階段是積分(從 0 到t) 的2*pi*f(t).f(t)定義如下。
參數 ::
返回 ::
注意:
該方法有四個選項。以下公式給出了chirp() 生成的信號的瞬時頻率(以赫茲為單位)。為方便起見,也可以使用下麵顯示的較短名稱。
linear, lin, li:
f(t) = f0 + (f1 - f0) * t / t1二次,四邊形,q:
The graph of the frequency f(t) is a parabola through (0, f0) and (t1, f1). By default, the vertex of the parabola is at (0, f0). If vertex_zero is False, then the vertex is at (t1, f1). The formula is:
if vertex_zero is True:
f(t) = f0 + (f1 - f0) * t**2 / t1**2else:
f(t) = f1 - (f1 - f0) * (t1 - t)**2 / t1**2To use a more general quadratic function, or an arbitrary polynomial, use the function
scipy.signal.sweep_poly.對數,log,lo:
f(t) = f0 * (f1/f0)**(t/t1)f0 and f1 must be nonzero and have the same sign.
This signal is also known as a geometric or exponential chirp.
雙曲線,炒作:
f(t) = f0*f1*t1 / ((f0 - f1)*t + f1*t1)f0 and f1 must be nonzero.
例子:
示例中將使用以下內容:
>>> import numpy as np >>> from scipy.signal import chirp, spectrogram >>> import matplotlib.pyplot as plt對於第一個示例,我們將繪製 10 秒內從 6 Hz 到 1 Hz 的線性啁啾的波形:
>>> t = np.linspace(0, 10, 1500) >>> w = chirp(t, f0=6, f1=1, t1=10, method='linear') >>> plt.plot(t, w) >>> plt.title("Linear Chirp, f(0)=6, f(10)=1") >>> plt.xlabel('t (sec)') >>> plt.show()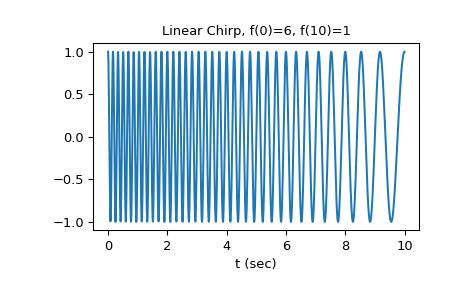
對於其餘示例,我們將使用更高的頻率範圍,並使用
scipy.signal.spectrogram演示結果。我們將使用以 7200 Hz 采樣的 4 秒間隔。>>> fs = 7200 >>> T = 4 >>> t = np.arange(0, int(T*fs)) / fs我們將使用這個函數來繪製每個示例中的頻譜圖。
>>> def plot_spectrogram(title, w, fs): ... ff, tt, Sxx = spectrogram(w, fs=fs, nperseg=256, nfft=576) ... fig, ax = plt.subplots() ... ax.pcolormesh(tt, ff[:145], Sxx[:145], cmap='gray_r', ... shading='gouraud') ... ax.set_title(title) ... ax.set_xlabel('t (sec)') ... ax.set_ylabel('Frequency (Hz)') ... ax.grid(True) ...從 1500 Hz 到 250 Hz 的二次啁啾(頻率拋物線的頂點在 t=0):
>>> w = chirp(t, f0=1500, f1=250, t1=T, method='quadratic') >>> plot_spectrogram(f'Quadratic Chirp, f(0)=1500, f({T})=250', w, fs) >>> plt.show()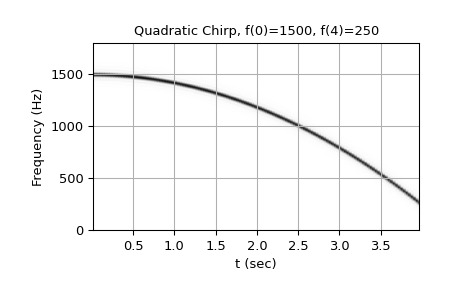
從 1500 Hz 到 250 Hz 的二次啁啾(頻率拋物線的頂點在 t=T):
>>> w = chirp(t, f0=1500, f1=250, t1=T, method='quadratic', ... vertex_zero=False) >>> plot_spectrogram(f'Quadratic Chirp, f(0)=1500, f({T})=250\n' + ... '(vertex_zero=False)', w, fs) >>> plt.show()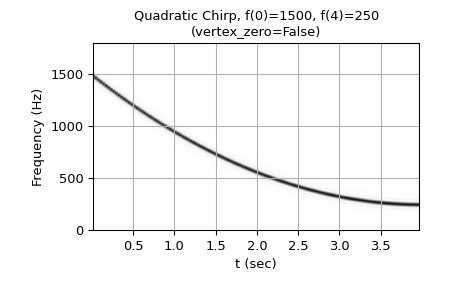
從 1500 Hz 到 250 Hz 的對數啁啾:
>>> w = chirp(t, f0=1500, f1=250, t1=T, method='logarithmic') >>> plot_spectrogram(f'Logarithmic Chirp, f(0)=1500, f({T})=250', w, fs) >>> plt.show()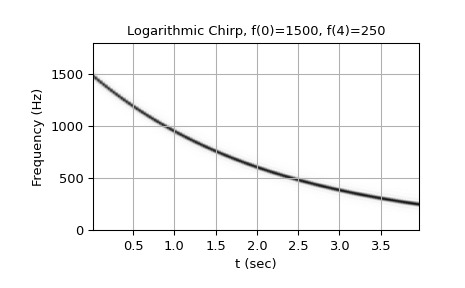
從 1500 Hz 到 250 Hz 的雙曲線啁啾:
>>> w = chirp(t, f0=1500, f1=250, t1=T, method='hyperbolic') >>> plot_spectrogram(f'Hyperbolic Chirp, f(0)=1500, f({T})=250', w, fs) >>> plt.show()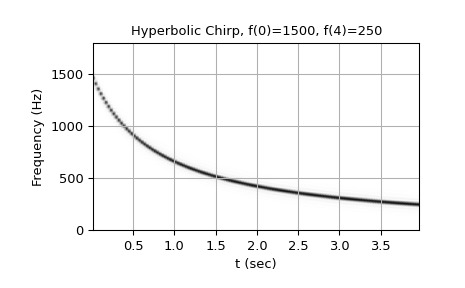
相關用法
- Python SciPy signal.cheb2ord用法及代碼示例
- Python SciPy signal.cheb1ord用法及代碼示例
- Python SciPy signal.cheby2用法及代碼示例
- Python SciPy signal.cheby1用法及代碼示例
- Python SciPy signal.check_COLA用法及代碼示例
- Python SciPy signal.choose_conv_method用法及代碼示例
- Python SciPy signal.check_NOLA用法及代碼示例
- Python SciPy signal.czt_points用法及代碼示例
- Python SciPy signal.coherence用法及代碼示例
- Python SciPy signal.csd用法及代碼示例
- Python SciPy signal.correlate2d用法及代碼示例
- Python SciPy signal.cubic用法及代碼示例
- Python SciPy signal.correlation_lags用法及代碼示例
- Python SciPy signal.convolve2d用法及代碼示例
- Python SciPy signal.cspline1d用法及代碼示例
- Python scipy.signal.czt用法及代碼示例
- Python SciPy signal.cwt用法及代碼示例
- Python SciPy signal.convolve用法及代碼示例
- Python SciPy signal.cont2discrete用法及代碼示例
- Python SciPy signal.cspline1d_eval用法及代碼示例
- Python SciPy signal.cmplx_sort用法及代碼示例
- Python SciPy signal.correlate用法及代碼示例
- Python SciPy signal.residue用法及代碼示例
- Python SciPy signal.iirdesign用法及代碼示例
- Python SciPy signal.max_len_seq用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.signal.chirp。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
