本文簡要介紹 python 語言中 scipy.signal.sweep_poly 的用法。
用法:
scipy.signal.sweep_poly(t, poly, phi=0)#Frequency-swept 餘弦發生器,具有與時間相關的頻率。
該函數生成一個正弦函數,其瞬時頻率隨時間變化。時間 t 的頻率由多項式 poly 給出。
- t: ndarray
評估波形的時間。
- poly: 一維 數組 或 numpy.poly1d 的實例
以多項式表示的所需頻率。如果 poly 是長度為 n 的列表或 ndarray,則 poly 的元素是多項式的係數,瞬時頻率為
f(t) = poly[0]*t**(n-1) + poly[1]*t**(n-2) + ... + poly[n-1]如果 poly 是 numpy.poly1d 的一個實例,則瞬時頻率為
f(t) = poly(t)- phi: 浮點數,可選
相位偏移,以度為單位,默認值:0。
- sweep_poly: ndarray
一個 numpy 數組,其中包含在t與請求的time-varying 頻率。更準確地說,函數返回
cos(phase + (pi/180)*phi),其中階段是積分(從 0 到 t)2 * pi * f(t);f(t)定義如上。
參數 ::
返回 ::
注意:
如果 poly 是長度為 n 的列表或 ndarray,則 poly 的元素是多項式的係數,瞬時頻率為:
f(t) = poly[0]*t**(n-1) + poly[1]*t**(n-2) + ... + poly[n-1]如果聚是一個實例numpy.poly1d,則瞬時頻率為:
f(t) = poly(t)最後,輸出 s 是:
cos(phase + (pi/180)*phi)其中階段是從 0 到的積分t的
2 * pi * f(t),f(t)如上定義。例子:
計算瞬時頻率的波形:
f(t) = 0.025*t**3 - 0.36*t**2 + 1.25*t + 2在 0 <= t <= 10 的區間內。
>>> import numpy as np >>> from scipy.signal import sweep_poly >>> p = np.poly1d([0.025, -0.36, 1.25, 2.0]) >>> t = np.linspace(0, 10, 5001) >>> w = sweep_poly(t, p)繪製它:
>>> import matplotlib.pyplot as plt >>> plt.subplot(2, 1, 1) >>> plt.plot(t, w) >>> plt.title("Sweep Poly\nwith frequency " + ... "$f(t) = 0.025t^3 - 0.36t^2 + 1.25t + 2$") >>> plt.subplot(2, 1, 2) >>> plt.plot(t, p(t), 'r', label='f(t)') >>> plt.legend() >>> plt.xlabel('t') >>> plt.tight_layout() >>> plt.show()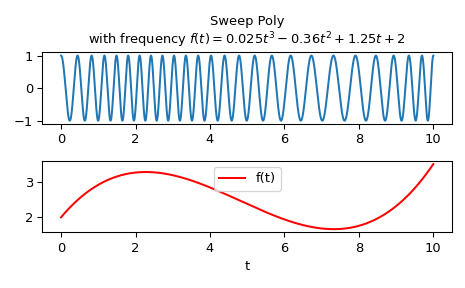
相關用法
- Python SciPy signal.step2用法及代碼示例
- Python SciPy signal.spectrogram用法及代碼示例
- Python SciPy signal.square用法及代碼示例
- Python SciPy signal.step用法及代碼示例
- Python SciPy signal.sosfiltfilt用法及代碼示例
- Python SciPy signal.savgol_coeffs用法及代碼示例
- Python SciPy signal.symiirorder1用法及代碼示例
- Python SciPy signal.sosfreqz用法及代碼示例
- Python SciPy signal.sosfilt用法及代碼示例
- Python SciPy signal.sosfilt_zi用法及代碼示例
- Python SciPy signal.sos2tf用法及代碼示例
- Python SciPy signal.sawtooth用法及代碼示例
- Python SciPy signal.symiirorder2用法及代碼示例
- Python SciPy signal.stft用法及代碼示例
- Python SciPy signal.ss2tf用法及代碼示例
- Python SciPy signal.savgol_filter用法及代碼示例
- Python SciPy signal.spline_filter用法及代碼示例
- Python SciPy signal.czt_points用法及代碼示例
- Python SciPy signal.chirp用法及代碼示例
- Python SciPy signal.residue用法及代碼示例
- Python SciPy signal.iirdesign用法及代碼示例
- Python SciPy signal.max_len_seq用法及代碼示例
- Python SciPy signal.kaiser_atten用法及代碼示例
- Python SciPy signal.oaconvolve用法及代碼示例
- Python SciPy signal.hilbert用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.signal.sweep_poly。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
