Python SciPy signal.stft用法及代碼示例

本文簡要介紹 python 語言中 scipy.signal.stft 的用法。

用法:

scipy.signal.stft(x, fs=1.0, window='hann', nperseg=256, noverlap=None, nfft=None, detrend=False, return_onesided=True, boundary='zeros', padded=True, axis=-1, scaling='spectrum')#

計算短時傅裏葉變換 (STFT)。

STFT 可用作量化非平穩信號的頻率和相位內容隨時間變化的一種方式。

遺產

此函數被視為遺留函數，將不再接收更新。這也可能意味著它將在未來的 SciPy 版本中被刪除。 ShortTimeFFT 是一個較新的 STFT /ISTFT 實現，具有更多函數。實現之間的比較可以在 SciPy 用戶指南的 Short-Time 傅裏葉變換部分找到。

參數 ：：

x： array_like

測量值的時間序列

fs： 浮點數，可選

x 時間序列的采樣頻率。默認為 1.0。

window： str 或 tuple 或 數組，可選

想要使用的窗口。如果窗戶是一個字符串或元組，它被傳遞給scipy.signal.get_window生成窗口值，默認為DFT-even。看scipy.signal.get_window獲取窗口列表和所需參數。如果窗戶是數組，它將直接用作窗口，其長度必須為nperseg。默認為 Hann 窗口。

nperseg： 整數，可選

每個段的長度。默認為 256。

noverlap： 整數，可選

段之間重疊的點數。如果None,noverlap = nperseg // 2.默認為None.指定時，必須滿足 COLA 約束(請參閱下麵的注釋)。

nfft： 整數，可選

如果需要零填充 FFT，則使用的 FFT 的長度。如果沒有，FFT 長度為 nperseg。默認為無。

detrend： str 或函數 或False， 可選的

指定如何去除每個段的趨勢。如果scipy.signal.detrend是一個字符串，它作為類型參數scipy.signal.detrend函數。如果它是一個函數，它接受一個段並返回一個去趨勢的段。如果scipy.signal.detrend是False，沒有去趨勢。默認為False.

return_onesided： 布爾型，可選

如果為 True，則返回真實數據的單側頻譜。如果為 False，則返回兩側頻譜。默認為 True，但對於複雜數據，始終返回兩側頻譜。

boundary： str 或無，可選

指定輸入信號是否在兩端擴展，以及如何生成新值，以使第一個窗口段居中於第一個輸入點。這具有在所采用的窗口函數從零開始時能夠重建第一個輸入點的好處。有效選項是 ['even', 'odd', 'constant', 'zeros', None] 。默認為‘zeros’，用於零填充擴展。 IE。 [1, 2, 3, 4] 擴展為 [0, 1, 2, 3, 4, 0] 用於 nperseg=3 。

padded： 布爾型，可選

指定輸入信號是否在末尾補零以使信號完全適合整數個窗口段，以便所有信號都包含在輸出中。默認為真。填充發生在邊界擴展之後，如果邊界不是無，填充為真，默認情況下。

axis： 整數，可選

計算 STFT 的軸；默認值在最後一個軸上(即 axis=-1 )。

scaling: {‘spectrum’, ‘psd’}：

默認的 ‘spectrum’ 縮放允許每個頻率線Zxx被解釋為幅度譜。 ‘psd’ 選項將每條線縮放到功率譜密度 - 它允許通過數字積分來計算信號能量abs(Zxx)**2.

返回 ：：

f： ndarray

采樣頻率數組。

t： ndarray

分段時間數組。

Zxx： ndarray

x 的 STFT。默認情況下，Zxx 的最後一個軸對應分段時間。

注意：

為了通過反 STFT 在scipy.signal.istft，信號加窗必須服從“Nonzero OverLap Add”(NOLA)的約束，輸入信號必須有完整的加窗覆蓋(即(x.shape[axis] - nperseg) % (nperseg-noverlap) == 0)。這軟填充參數可以用來實現這一點。

給定 time-domain 信號\(x[n]\)， 一個窗口\(w[n]\), 和跳數\(H\)=nperseg - 非重疊, 時間索引處的窗口幀\(t\)是(誰)給的

\[x_{t}[n]=x[n]w[n-tH]\]

overlap-add (OLA) 重建方程由下式給出

\[x[n]=\frac{\sum_{t}x_{t}[n]w[n-tH]}{\sum_{t}w^{2}[n-tH]}\]

NOLA 約束確保出現在 OLA 重建方程的分母中的每個歸一化項都是非零的。無論是選擇窗戶,nperseg， 和重疊滿足這個約束可以用scipy.signal.check_NOLA.

參考：

[1]

Oppenheim、Alan V.、Ronald W. Schafer、John R. Buck “Discrete-Time 信號處理”，Prentice Hall，1999 年。

[2]

Daniel W. Griffin, Jae S. Lim “信號估計來自修改的 Short-Time Fourier Transform”，IEEE 1984, 10.1109/TASSP.1984.1164317

例子：

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()

生成一個測試信號，一個 2 Vrms 正弦波，其頻率在 3kHz 左右緩慢調製，被以 10kHz 采樣的呈 index 下降幅度的白噪聲破壞。

>>> fs = 10e3
>>> N = 1e5
>>> amp = 2 * np.sqrt(2)
>>> noise_power = 0.01 * fs / 2
>>> time = np.arange(N) / float(fs)
>>> mod = 500*np.cos(2*np.pi*0.25*time)
>>> carrier = amp * np.sin(2*np.pi*3e3*time + mod)
>>> noise = rng.normal(scale=np.sqrt(noise_power),
...                    size=time.shape)
>>> noise *= np.exp(-time/5)
>>> x = carrier + noise

計算並繪製 STFT 的大小。

>>> f, t, Zxx = signal.stft(x, fs, nperseg=1000)
>>> plt.pcolormesh(t, f, np.abs(Zxx), vmin=0, vmax=amp, shading='gouraud')
>>> plt.title('STFT Magnitude')
>>> plt.ylabel('Frequency [Hz]')
>>> plt.xlabel('Time [sec]')
>>> plt.show()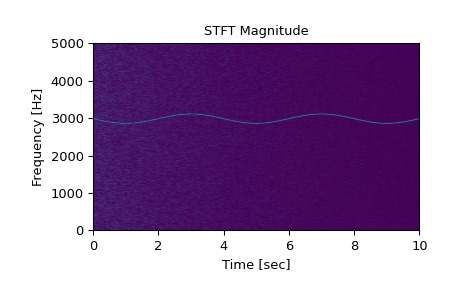

將信號 x 的能量與其 STFT 的能量進行比較：

>>> E_x = sum(x**2) / fs  # Energy of x
>>> # Calculate a two-sided STFT with PSD scaling:
>>> f, t, Zxx = signal.stft(x, fs, nperseg=1000, return_onesided=False,
...                         scaling='psd')
>>> # Integrate numerically over abs(Zxx)**2:
>>> df, dt = f[1] - f[0], t[1] - t[0]
>>> E_Zxx = sum(np.sum(Zxx.real**2 + Zxx.imag**2, axis=0) * df) * dt
>>> # The energy is the same, but the numerical errors are quite large:
>>> np.isclose(E_x, E_Zxx, rtol=1e-2)
True