Python SciPy signal.stft用法及代码示例

本文简要介绍 python 语言中 scipy.signal.stft 的用法。

用法:

scipy.signal.stft(x, fs=1.0, window='hann', nperseg=256, noverlap=None, nfft=None, detrend=False, return_onesided=True, boundary='zeros', padded=True, axis=-1, scaling='spectrum')#

计算短时傅里叶变换 (STFT)。

STFT 可用作量化非平稳信号的频率和相位内容随时间变化的一种方式。

遗产

此函数被视为遗留函数，将不再接收更新。这也可能意味着它将在未来的 SciPy 版本中被删除。 ShortTimeFFT 是一个较新的 STFT /ISTFT 实现，具有更多函数。实现之间的比较可以在 SciPy 用户指南的 Short-Time 傅里叶变换部分找到。

参数 ：：

x： array_like

测量值的时间序列

fs： 浮点数，可选

x 时间序列的采样频率。默认为 1.0。

window： str 或 tuple 或 数组，可选

想要使用的窗口。如果窗户是一个字符串或元组，它被传递给scipy.signal.get_window生成窗口值，默认为DFT-even。看scipy.signal.get_window获取窗口列表和所需参数。如果窗户是数组，它将直接用作窗口，其长度必须为nperseg。默认为 Hann 窗口。

nperseg： 整数，可选

每个段的长度。默认为 256。

noverlap： 整数，可选

段之间重叠的点数。如果None,noverlap = nperseg // 2.默认为None.指定时，必须满足 COLA 约束(请参阅下面的注释)。

nfft： 整数，可选

如果需要零填充 FFT，则使用的 FFT 的长度。如果没有，FFT 长度为 nperseg。默认为无。

detrend： str 或函数 或False， 可选的

指定如何去除每个段的趋势。如果scipy.signal.detrend是一个字符串，它作为类型参数scipy.signal.detrend函数。如果它是一个函数，它接受一个段并返回一个去趋势的段。如果scipy.signal.detrend是False，没有去趋势。默认为False.

return_onesided： 布尔型，可选

如果为 True，则返回真实数据的单侧频谱。如果为 False，则返回两侧频谱。默认为 True，但对于复杂数据，始终返回两侧频谱。

boundary： str 或无，可选

指定输入信号是否在两端扩展，以及如何生成新值，以使第一个窗口段居中于第一个输入点。这具有在所采用的窗口函数从零开始时能够重建第一个输入点的好处。有效选项是 ['even', 'odd', 'constant', 'zeros', None] 。默认为‘zeros’，用于零填充扩展。 IE。 [1, 2, 3, 4] 扩展为 [0, 1, 2, 3, 4, 0] 用于 nperseg=3 。

padded： 布尔型，可选

指定输入信号是否在末尾补零以使信号完全适合整数个窗口段，以便所有信号都包含在输出中。默认为真。填充发生在边界扩展之后，如果边界不是无，填充为真，默认情况下。

axis： 整数，可选

计算 STFT 的轴；默认值在最后一个轴上(即 axis=-1 )。

scaling: {‘spectrum’, ‘psd’}：

默认的 ‘spectrum’ 缩放允许每个频率线Zxx被解释为幅度谱。 ‘psd’ 选项将每条线缩放到功率谱密度 - 它允许通过数字积分来计算信号能量abs(Zxx)**2.

返回 ：：

f： ndarray

采样频率数组。

t： ndarray

分段时间数组。

Zxx： ndarray

x 的 STFT。默认情况下，Zxx 的最后一个轴对应分段时间。

注意：

为了通过反 STFT 在scipy.signal.istft，信号加窗必须服从“Nonzero OverLap Add”(NOLA)的约束，输入信号必须有完整的加窗覆盖(即(x.shape[axis] - nperseg) % (nperseg-noverlap) == 0)。这软填充参数可以用来实现这一点。

给定 time-domain 信号\(x[n]\)， 一个窗口\(w[n]\), 和跳数\(H\)=nperseg - 非重叠, 时间索引处的窗口帧\(t\)是(谁)给的

\[x_{t}[n]=x[n]w[n-tH]\]

overlap-add (OLA) 重建方程由下式给出

\[x[n]=\frac{\sum_{t}x_{t}[n]w[n-tH]}{\sum_{t}w^{2}[n-tH]}\]

NOLA 约束确保出现在 OLA 重建方程的分母中的每个归一化项都是非零的。无论是选择窗户,nperseg， 和重叠满足这个约束可以用scipy.signal.check_NOLA.

参考：

[1]

Oppenheim、Alan V.、Ronald W. Schafer、John R. Buck “Discrete-Time 信号处理”，Prentice Hall，1999 年。

[2]

Daniel W. Griffin, Jae S. Lim “信号估计来自修改的 Short-Time Fourier Transform”，IEEE 1984, 10.1109/TASSP.1984.1164317

例子：

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()

生成一个测试信号，一个 2 Vrms 正弦波，其频率在 3kHz 左右缓慢调制，被以 10kHz 采样的呈 index 下降幅度的白噪声破坏。

>>> fs = 10e3
>>> N = 1e5
>>> amp = 2 * np.sqrt(2)
>>> noise_power = 0.01 * fs / 2
>>> time = np.arange(N) / float(fs)
>>> mod = 500*np.cos(2*np.pi*0.25*time)
>>> carrier = amp * np.sin(2*np.pi*3e3*time + mod)
>>> noise = rng.normal(scale=np.sqrt(noise_power),
...                    size=time.shape)
>>> noise *= np.exp(-time/5)
>>> x = carrier + noise

计算并绘制 STFT 的大小。

>>> f, t, Zxx = signal.stft(x, fs, nperseg=1000)
>>> plt.pcolormesh(t, f, np.abs(Zxx), vmin=0, vmax=amp, shading='gouraud')
>>> plt.title('STFT Magnitude')
>>> plt.ylabel('Frequency [Hz]')
>>> plt.xlabel('Time [sec]')
>>> plt.show()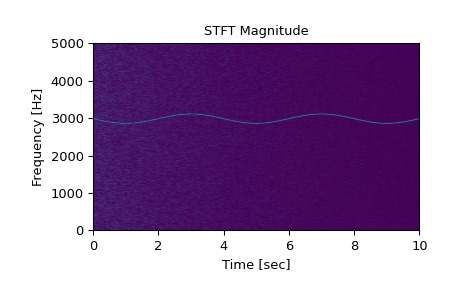

将信号 x 的能量与其 STFT 的能量进行比较：

>>> E_x = sum(x**2) / fs  # Energy of x
>>> # Calculate a two-sided STFT with PSD scaling:
>>> f, t, Zxx = signal.stft(x, fs, nperseg=1000, return_onesided=False,
...                         scaling='psd')
>>> # Integrate numerically over abs(Zxx)**2:
>>> df, dt = f[1] - f[0], t[1] - t[0]
>>> E_Zxx = sum(np.sum(Zxx.real**2 + Zxx.imag**2, axis=0) * df) * dt
>>> # The energy is the same, but the numerical errors are quite large:
>>> np.isclose(E_x, E_Zxx, rtol=1e-2)
True