本文简要介绍 python 语言中 scipy.signal.hilbert 的用法。
用法:
scipy.signal.hilbert(x, N=None, axis=-1)#使用希尔伯特变换计算解析信号。
默认情况下,转换沿最后一个轴完成。
- x: array_like
信号数据。一定是真的。
- N: 整数,可选
傅里叶分量的数量。默认值:
x.shape[axis]- axis: 整数,可选
沿其进行转换的轴。默认值:-1。
- xa: ndarray
沿轴的每个一维阵列的 x 的解析信号
参数 ::
返回 ::
注意:
信号
x(t)的解析信号x_a(t)为:其中F是傅里叶变换,U单位阶跃函数,和y希尔伯特变换x.[1]
换句话说,频谱的负半部分被归零,将实值信号变为复信号。希尔伯特变换信号可以从
np.imag(hilbert(x))获得,原始信号可以从np.real(hilbert(x))获得。参考:
[1]维基百科,“Analytic signal”。 https://en.wikipedia.org/wiki/Analytic_signal
[2]Leon Cohen,“Time-Frequency 分析”,1995 年。第 2 章。
[3]艾伦·V·奥本海姆、罗纳德·W·谢弗。 Discrete-Time 信号处理,第三版,2009 年。第 12 章。ISBN 13:978-1292-02572-8
例子:
在本例中,我们使用希尔伯特变换来确定amplitude-modulated 信号的幅度包络和瞬时频率。
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy.signal import hilbert, chirp>>> duration = 1.0 >>> fs = 400.0 >>> samples = int(fs*duration) >>> t = np.arange(samples) / fs我们创建一个频率从 20 Hz 增加到 100 Hz 的啁啾,并应用幅度调制。
>>> signal = chirp(t, 20.0, t[-1], 100.0) >>> signal *= (1.0 + 0.5 * np.sin(2.0*np.pi*3.0*t) )幅度包络由分析信号的幅度给出。瞬时频率可以通过瞬时相位对时间的微分获得。瞬时相位对应于解析信号的相位角。
>>> analytic_signal = hilbert(signal) >>> amplitude_envelope = np.abs(analytic_signal) >>> instantaneous_phase = np.unwrap(np.angle(analytic_signal)) >>> instantaneous_frequency = (np.diff(instantaneous_phase) / ... (2.0*np.pi) * fs)>>> fig, (ax0, ax1) = plt.subplots(nrows=2) >>> ax0.plot(t, signal, label='signal') >>> ax0.plot(t, amplitude_envelope, label='envelope') >>> ax0.set_xlabel("time in seconds") >>> ax0.legend() >>> ax1.plot(t[1:], instantaneous_frequency) >>> ax1.set_xlabel("time in seconds") >>> ax1.set_ylim(0.0, 120.0) >>> fig.tight_layout()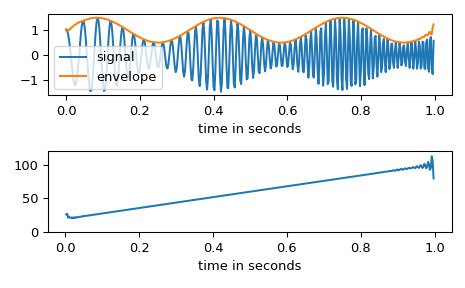
相关用法
- Python SciPy signal.czt_points用法及代码示例
- Python SciPy signal.chirp用法及代码示例
- Python SciPy signal.residue用法及代码示例
- Python SciPy signal.iirdesign用法及代码示例
- Python SciPy signal.max_len_seq用法及代码示例
- Python SciPy signal.kaiser_atten用法及代码示例
- Python SciPy signal.oaconvolve用法及代码示例
- Python SciPy signal.ricker用法及代码示例
- Python SciPy signal.group_delay用法及代码示例
- Python SciPy signal.cheb2ord用法及代码示例
- Python SciPy signal.get_window用法及代码示例
- Python SciPy signal.lfilter用法及代码示例
- Python SciPy signal.morlet用法及代码示例
- Python SciPy signal.coherence用法及代码示例
- Python SciPy signal.dfreqresp用法及代码示例
- Python SciPy signal.TransferFunction用法及代码示例
- Python SciPy signal.dbode用法及代码示例
- Python SciPy signal.residuez用法及代码示例
- Python SciPy signal.bilinear_zpk用法及代码示例
- Python SciPy signal.firls用法及代码示例
- Python SciPy signal.impulse用法及代码示例
- Python SciPy signal.buttord用法及代码示例
- Python SciPy signal.find_peaks用法及代码示例
- Python SciPy signal.freqs用法及代码示例
- Python SciPy signal.step2用法及代码示例
注:本文由纯净天空筛选整理自scipy.org大神的英文原创作品 scipy.signal.hilbert。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
