本文简要介绍 python 语言中 scipy.signal.istft 的用法。
用法:
scipy.signal.istft(Zxx, fs=1.0, window='hann', nperseg=None, noverlap=None, nfft=None, input_onesided=True, boundary=True, time_axis=-1, freq_axis=-2, scaling='spectrum')#执行逆短时傅里叶变换 (iSTFT)。
遗产
此函数被视为遗留函数,将不再接收更新。这也可能意味着它将在未来的 SciPy 版本中被删除。
ShortTimeFFT是一个较新的 STFT /ISTFT 实现,具有更多函数。实现之间的比较可以在 SciPy 用户指南的 Short-Time 傅里叶变换部分找到。- Zxx: array_like
要重建的信号的 STFT。如果传递的是纯实数数组,它将被强制转换为复杂数据类型。
- fs: 浮点数,可选
时间序列的采样频率。默认为 1.0。
- window: str 或 tuple 或 数组,可选
想要使用的窗口。如果窗户是一个字符串或元组,它被传递给scipy.signal.get_window生成窗口值,默认为DFT-even。看scipy.signal.get_window获取窗口列表和所需参数。如果窗户是数组,它将直接用作窗口,其长度必须为nperseg。默认为 Hann 窗口。必须与用于生成 STFT 的窗口匹配以实现忠实的反演。
- nperseg: 整数,可选
每个 STFT 段对应的数据点数。如果每段的数据点数是奇数,或者如果 STFT 是通过填充的,则必须指定此参数
nfft > nperseg.如果None,值取决于形状Zxx和input_onesided.如果input_onesided是True,nperseg=2*(Zxx.shape[freq_axis] - 1).否则,nperseg=Zxx.shape[freq_axis].默认为None.- noverlap: 整数,可选
段之间重叠的点数。如果没有,则为段长度的一半。默认为无。指定时,必须满足 COLA 约束(请参阅下面的注释),并且应与用于生成 STFT 的参数匹配。默认为无。
- nfft: 整数,可选
每个 STFT 段对应的 FFT 点数。如果 STFT 通过以下方式填充,则必须指定此参数
nfft > nperseg.如果None, 默认值与nperseg,上面详述,但有一个异常:如果input_onesided是真的并且nperseg==2*Zxx.shape[freq_axis] - 1,nfft也具有该值。这种情况允许使用 odd-length 未填充的 STFT 正确反转nfft=None.默认为None.- input_onesided: 布尔型,可选
如果True,将输入数组解释为单边 FFT,例如由scipy.signal.stft和
return_onesided=True和numpy.fft.rfft.如果False,将输入解释为双边 FFT。默认为True.- boundary: 布尔型,可选
指定输入信号是否在其边界处通过提供非扩展None
boundary参数scipy.signal.stft.默认为True.- time_axis: 整数,可选
STFT的时间段所在的位置;默认值为最后一个轴(即
axis=-1)。- freq_axis: 整数,可选
STFT的频率轴所在的位置;默认值为倒数第二个轴(即
axis=-2)。- scaling: {‘spectrum’, ‘psd’}:
默认的 ‘spectrum’ 缩放允许每个频率线Zxx被解释为幅度谱。 ‘psd’ 选项将每条线缩放到功率谱密度 - 它允许通过数字积分来计算信号能量
abs(Zxx)**2.
- t: ndarray
输出数据时间数组。
- x: ndarray
Zxx 的 iSTFT。
参数 ::
返回 ::
注意:
为了通过
istft实现 STFT 的反转,信号加窗必须遵守 “nonzero overlap add” (NOLA) 的约束:这确保了出现在 overlap-add 重建方程的分母中的归一化因子
不为零。可以使用
check_NOLA函数检查 NOLA 约束。已修改(通过掩蔽或其他方式)的 STFT 不能保证对应于完全可实现的信号。该函数通过[2]中详述的最小二乘估计算法实现 iSTFT,该算法产生的信号可最小化返回信号的 STFT 与修改后的 STFT 之间的均方误差。
参考:
[1]Oppenheim、Alan V.、Ronald W. Schafer、John R. Buck “Discrete-Time 信号处理”,Prentice Hall,1999 年。
[2]Daniel W. Griffin, Jae S. Lim “信号估计来自修改的 Short-Time Fourier Transform”,IEEE 1984, 10.1109/TASSP.1984.1164317
例子:
>>> import numpy as np >>> from scipy import signal >>> import matplotlib.pyplot as plt >>> rng = np.random.default_rng()生成一个测试信号,一个 50Hz 的 2 Vrms 正弦波,被 1024 Hz 采样的 0.001 V**2/Hz 白噪声破坏。
>>> fs = 1024 >>> N = 10*fs >>> nperseg = 512 >>> amp = 2 * np.sqrt(2) >>> noise_power = 0.001 * fs / 2 >>> time = np.arange(N) / float(fs) >>> carrier = amp * np.sin(2*np.pi*50*time) >>> noise = rng.normal(scale=np.sqrt(noise_power), ... size=time.shape) >>> x = carrier + noise计算 STFT,并绘制其大小
>>> f, t, Zxx = signal.stft(x, fs=fs, nperseg=nperseg) >>> plt.figure() >>> plt.pcolormesh(t, f, np.abs(Zxx), vmin=0, vmax=amp, shading='gouraud') >>> plt.ylim([f[1], f[-1]]) >>> plt.title('STFT Magnitude') >>> plt.ylabel('Frequency [Hz]') >>> plt.xlabel('Time [sec]') >>> plt.yscale('log') >>> plt.show()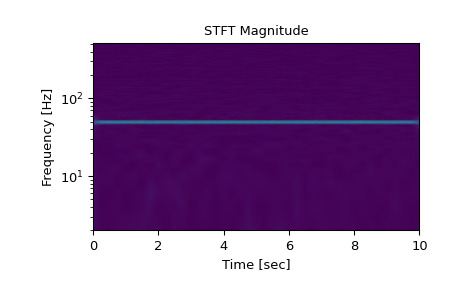
将小于或等于载波幅度 10% 的分量归零,然后通过逆 STFT 转换回时间序列
>>> Zxx = np.where(np.abs(Zxx) >= amp/10, Zxx, 0) >>> _, xrec = signal.istft(Zxx, fs)将清洁后的信号与原始和真实的载波信号进行比较。
>>> plt.figure() >>> plt.plot(time, x, time, xrec, time, carrier) >>> plt.xlim([2, 2.1]) >>> plt.xlabel('Time [sec]') >>> plt.ylabel('Signal') >>> plt.legend(['Carrier + Noise', 'Filtered via STFT', 'True Carrier']) >>> plt.show()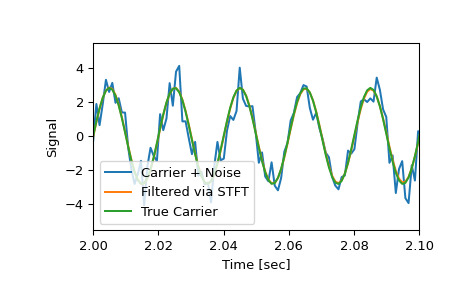
请注意,清理后的信号不会像原始信号那样突然开始,因为还删除了一些瞬态系数:
>>> plt.figure() >>> plt.plot(time, x, time, xrec, time, carrier) >>> plt.xlim([0, 0.1]) >>> plt.xlabel('Time [sec]') >>> plt.ylabel('Signal') >>> plt.legend(['Carrier + Noise', 'Filtered via STFT', 'True Carrier']) >>> plt.show()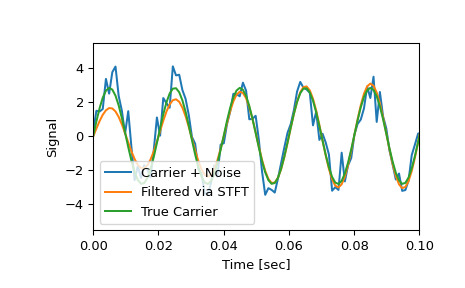
相关用法
- Python SciPy signal.iirdesign用法及代码示例
- Python SciPy signal.impulse用法及代码示例
- Python SciPy signal.iirfilter用法及代码示例
- Python SciPy signal.impulse2用法及代码示例
- Python SciPy signal.invresz用法及代码示例
- Python SciPy signal.iirnotch用法及代码示例
- Python SciPy signal.iircomb用法及代码示例
- Python SciPy signal.invres用法及代码示例
- Python SciPy signal.iirpeak用法及代码示例
- Python SciPy signal.czt_points用法及代码示例
- Python SciPy signal.chirp用法及代码示例
- Python SciPy signal.residue用法及代码示例
- Python SciPy signal.max_len_seq用法及代码示例
- Python SciPy signal.kaiser_atten用法及代码示例
- Python SciPy signal.oaconvolve用法及代码示例
- Python SciPy signal.hilbert用法及代码示例
- Python SciPy signal.ricker用法及代码示例
- Python SciPy signal.group_delay用法及代码示例
- Python SciPy signal.cheb2ord用法及代码示例
- Python SciPy signal.get_window用法及代码示例
- Python SciPy signal.lfilter用法及代码示例
- Python SciPy signal.morlet用法及代码示例
- Python SciPy signal.coherence用法及代码示例
- Python SciPy signal.dfreqresp用法及代码示例
- Python SciPy signal.TransferFunction用法及代码示例
注:本文由纯净天空筛选整理自scipy.org大神的英文原创作品 scipy.signal.istft。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
