本文简要介绍 python 语言中 scipy.signal.spectrogram 的用法。
用法:
scipy.signal.spectrogram(x, fs=1.0, window=('tukey', 0.25), nperseg=None, noverlap=None, nfft=None, detrend='constant', return_onesided=True, scaling='density', axis=-1, mode='psd')#计算具有连续傅里叶变换的频谱图。
频谱图可用作可视化非平稳信号频率内容随时间变化的一种方式。
遗产
此函数被视为遗留函数,将不再接收更新。这也可能意味着它将在未来的 SciPy 版本中被删除。
ShortTimeFFT是较新的 STFT /ISTFT 实现,具有更多函数,还包括spectrogram方法。实现之间的比较可以在 SciPy 用户指南的 Short-Time 傅里叶变换部分找到。- x: array_like
测量值的时间序列
- fs: 浮点数,可选
x 时间序列的采样频率。默认为 1.0。
- window: str 或 tuple 或 数组,可选
想要使用的窗口。如果窗户是一个字符串或元组,它被传递给scipy.signal.get_window生成窗口值,默认为DFT-even。看scipy.signal.get_window获取窗口列表和所需参数。如果窗户是数组,它将直接用作窗口,其长度必须为nperseg。默认为形状参数为 0.25 的 Tukey 窗口。
- nperseg: 整数,可选
每个段的长度。默认为 None,但如果 window 是 str 或 tuple,则设置为 256,如果 window 是 数组,则设置为窗口的长度。
- noverlap: 整数,可选
段之间重叠的点数。如果None,
noverlap = nperseg // 8.默认为None.- nfft: 整数,可选
如果需要零填充 FFT,则使用的 FFT 的长度。如果没有,FFT 长度为 nperseg。默认为无。
- detrend: str 或函数 或False, 可选的
指定如何去除每个段的趋势。如果scipy.signal.detrend是一个字符串,它作为类型参数scipy.signal.detrend函数。如果它是一个函数,它接受一个段并返回一个去趋势的段。如果scipy.signal.detrend是False,没有去趋势。默认为‘constant’。
- return_onesided: 布尔型,可选
如果为 True,则返回真实数据的单侧频谱。如果为 False,则返回两侧频谱。默认为 True,但对于复杂数据,始终返回两侧频谱。
- scaling: { ‘density’, ‘spectrum’ },可选
在计算 Sxx 的单位为 V**2/Hz 的功率谱密度 (‘density’) 和计算 Sxx 的单位为 V**2 的功率谱 (‘spectrum’) 之间进行选择,如果 x 以 V 为单位测量并且fs 以赫兹为单位。默认为‘density’。
- axis: 整数,可选
计算频谱图的轴;默认值在最后一个轴上(即
axis=-1)。- mode: str,可选
定义期望的返回值类型。选项是[‘psd’, ‘complex’, ‘magnitude’, ‘angle’, ‘phase’]。 ‘complex’ 相当于
stft的输出,没有填充或边界扩展。 ‘magnitude’ 返回 STFT 的绝对幅度。 ‘angle’ 和 ‘phase’ 分别返回 STFT 的复角(展开和不展开)。
- f: ndarray
采样频率数组。
- t: ndarray
分段时间数组。
- Sxx: ndarray
x 的频谱图。默认情况下,Sxx 的最后一个轴对应分段时间。
参数 ::
返回 ::
注意:
适当的重叠量取决于窗口的选择和您的要求。与 welch 的方法(其中整个数据流被平均)相比,人们可能希望在计算频谱图时使用较小的重叠(或者可能根本没有重叠),以保持各个片段之间的一些统计独立性。正是由于这个原因,默认窗口是一个 Tukey 窗口,每端有 1/8 的窗口长度重叠。
参考:
[1]Oppenheim、Alan V.、Ronald W. Schafer、John R. Buck “Discrete-Time 信号处理”,Prentice Hall,1999 年。
例子:
>>> import numpy as np >>> from scipy import signal >>> from scipy.fft import fftshift >>> import matplotlib.pyplot as plt >>> rng = np.random.default_rng()生成一个测试信号,一个 2 Vrms 正弦波,其频率在 3kHz 左右缓慢调制,被以 10kHz 采样的呈 index 下降幅度的白噪声破坏。
>>> fs = 10e3 >>> N = 1e5 >>> amp = 2 * np.sqrt(2) >>> noise_power = 0.01 * fs / 2 >>> time = np.arange(N) / float(fs) >>> mod = 500*np.cos(2*np.pi*0.25*time) >>> carrier = amp * np.sin(2*np.pi*3e3*time + mod) >>> noise = rng.normal(scale=np.sqrt(noise_power), size=time.shape) >>> noise *= np.exp(-time/5) >>> x = carrier + noise计算并绘制频谱图。
>>> f, t, Sxx = signal.spectrogram(x, fs) >>> plt.pcolormesh(t, f, Sxx, shading='gouraud') >>> plt.ylabel('Frequency [Hz]') >>> plt.xlabel('Time [sec]') >>> plt.show()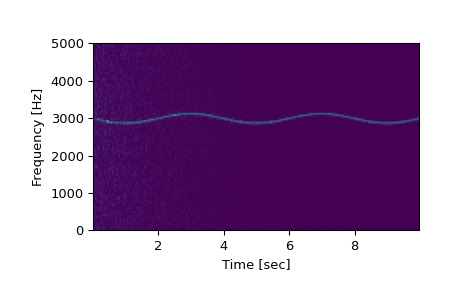
请注意,如果使用不是单侧的输出,则使用以下内容:
>>> f, t, Sxx = signal.spectrogram(x, fs, return_onesided=False) >>> plt.pcolormesh(t, fftshift(f), fftshift(Sxx, axes=0), shading='gouraud') >>> plt.ylabel('Frequency [Hz]') >>> plt.xlabel('Time [sec]') >>> plt.show()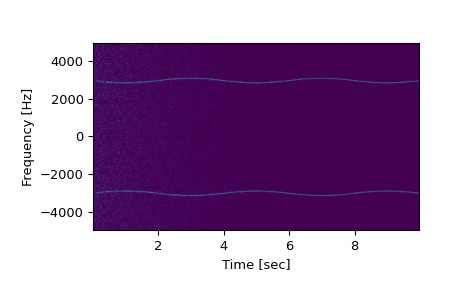
相关用法
- Python SciPy signal.spline_filter用法及代码示例
- Python SciPy signal.step2用法及代码示例
- Python SciPy signal.square用法及代码示例
- Python SciPy signal.step用法及代码示例
- Python SciPy signal.sweep_poly用法及代码示例
- Python SciPy signal.sosfiltfilt用法及代码示例
- Python SciPy signal.savgol_coeffs用法及代码示例
- Python SciPy signal.symiirorder1用法及代码示例
- Python SciPy signal.sosfreqz用法及代码示例
- Python SciPy signal.sosfilt用法及代码示例
- Python SciPy signal.sosfilt_zi用法及代码示例
- Python SciPy signal.sos2tf用法及代码示例
- Python SciPy signal.sawtooth用法及代码示例
- Python SciPy signal.symiirorder2用法及代码示例
- Python SciPy signal.stft用法及代码示例
- Python SciPy signal.ss2tf用法及代码示例
- Python SciPy signal.savgol_filter用法及代码示例
- Python SciPy signal.czt_points用法及代码示例
- Python SciPy signal.chirp用法及代码示例
- Python SciPy signal.residue用法及代码示例
- Python SciPy signal.iirdesign用法及代码示例
- Python SciPy signal.max_len_seq用法及代码示例
- Python SciPy signal.kaiser_atten用法及代码示例
- Python SciPy signal.oaconvolve用法及代码示例
- Python SciPy signal.hilbert用法及代码示例
注:本文由纯净天空筛选整理自scipy.org大神的英文原创作品 scipy.signal.spectrogram。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
