本文簡要介紹 python 語言中 scipy.signal.sosfreqz 的用法。
用法:
scipy.signal.sosfreqz(sos, worN=512, whole=False, fs=6.283185307179586)#以 SOS 格式計算數字濾波器的頻率響應。
給定 sos,一個形狀為 (n, 6) 的數字濾波器二階部分的數組,計算係統函數的頻率響應:
B0(z) B1(z) B{n-1}(z) H(z) = ----- * ----- * ... * --------- A0(z) A1(z) A{n-1}(z)對於 z = exp(omega*1j),其中 B{k}(z) 和 A{k}(z) 是 k-th 二階部分的傳遞函數的分子和分母。
- sos: array_like
二階濾波器係數數組,必須具有形狀
(n_sections, 6)。每行對應一個二階部分,前三列提供分子係數,後三列提供分母係數。- worN: {無,int,數組},可選
如果是單個整數,則以那麽多頻率進行計算(默認為 N=512)。對 FFT 計算使用快速的數字可以導致更快的計算(請參閱
freqz的注釋)。如果是 數組,計算給定頻率的響應(必須是 1-D)。這些與 fs 的單位相同。
- whole: 布爾型,可選
通常,頻率的計算範圍是從 0 到奈奎斯特頻率 fs/2(upper-half of unit-circle)。如果整體為真,則計算從 0 到 fs 的頻率。
- fs: 浮點數,可選
數字係統的采樣頻率。默認為 2*pi 弧度/樣本(所以 w 是從 0 到 pi)。
- w: ndarray
計算 h 的頻率,單位與 fs 相同。默認情況下,w 被歸一化為範圍 [0, pi)(弧度/樣本)。
- h: ndarray
頻率響應,作為複數。
參數 ::
返回 ::
注意:
例子:
設計一個 SOS 格式的 15th-order 帶通濾波器。
>>> from scipy import signal >>> import numpy as np >>> sos = signal.ellip(15, 0.5, 60, (0.2, 0.4), btype='bandpass', ... output='sos')計算從 DC 到 Nyquist 的 1500 個點的頻率響應。
>>> w, h = signal.sosfreqz(sos, worN=1500)繪製響應。
>>> import matplotlib.pyplot as plt >>> plt.subplot(2, 1, 1) >>> db = 20*np.log10(np.maximum(np.abs(h), 1e-5)) >>> plt.plot(w/np.pi, db) >>> plt.ylim(-75, 5) >>> plt.grid(True) >>> plt.yticks([0, -20, -40, -60]) >>> plt.ylabel('Gain [dB]') >>> plt.title('Frequency Response') >>> plt.subplot(2, 1, 2) >>> plt.plot(w/np.pi, np.angle(h)) >>> plt.grid(True) >>> plt.yticks([-np.pi, -0.5*np.pi, 0, 0.5*np.pi, np.pi], ... [r'$-\pi$', r'$-\pi/2$', '0', r'$\pi/2$', r'$\pi$']) >>> plt.ylabel('Phase [rad]') >>> plt.xlabel('Normalized frequency (1.0 = Nyquist)') >>> plt.show()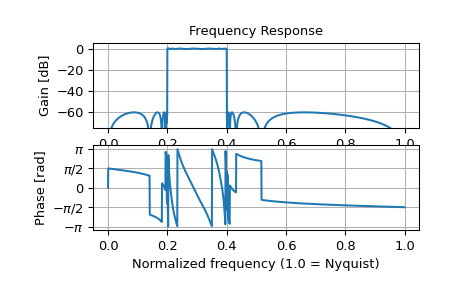
如果將相同的濾波器實現為單個傳遞函數,則數值誤差會破壞頻率響應:
>>> b, a = signal.ellip(15, 0.5, 60, (0.2, 0.4), btype='bandpass', ... output='ba') >>> w, h = signal.freqz(b, a, worN=1500) >>> plt.subplot(2, 1, 1) >>> db = 20*np.log10(np.maximum(np.abs(h), 1e-5)) >>> plt.plot(w/np.pi, db) >>> plt.ylim(-75, 5) >>> plt.grid(True) >>> plt.yticks([0, -20, -40, -60]) >>> plt.ylabel('Gain [dB]') >>> plt.title('Frequency Response') >>> plt.subplot(2, 1, 2) >>> plt.plot(w/np.pi, np.angle(h)) >>> plt.grid(True) >>> plt.yticks([-np.pi, -0.5*np.pi, 0, 0.5*np.pi, np.pi], ... [r'$-\pi$', r'$-\pi/2$', '0', r'$\pi/2$', r'$\pi$']) >>> plt.ylabel('Phase [rad]') >>> plt.xlabel('Normalized frequency (1.0 = Nyquist)') >>> plt.show()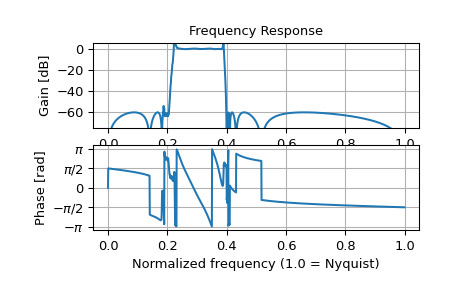
相關用法
- Python SciPy signal.sosfiltfilt用法及代碼示例
- Python SciPy signal.sosfilt用法及代碼示例
- Python SciPy signal.sosfilt_zi用法及代碼示例
- Python SciPy signal.sos2tf用法及代碼示例
- Python SciPy signal.step2用法及代碼示例
- Python SciPy signal.spectrogram用法及代碼示例
- Python SciPy signal.square用法及代碼示例
- Python SciPy signal.step用法及代碼示例
- Python SciPy signal.sweep_poly用法及代碼示例
- Python SciPy signal.savgol_coeffs用法及代碼示例
- Python SciPy signal.symiirorder1用法及代碼示例
- Python SciPy signal.sawtooth用法及代碼示例
- Python SciPy signal.symiirorder2用法及代碼示例
- Python SciPy signal.stft用法及代碼示例
- Python SciPy signal.ss2tf用法及代碼示例
- Python SciPy signal.savgol_filter用法及代碼示例
- Python SciPy signal.spline_filter用法及代碼示例
- Python SciPy signal.czt_points用法及代碼示例
- Python SciPy signal.chirp用法及代碼示例
- Python SciPy signal.residue用法及代碼示例
- Python SciPy signal.iirdesign用法及代碼示例
- Python SciPy signal.max_len_seq用法及代碼示例
- Python SciPy signal.kaiser_atten用法及代碼示例
- Python SciPy signal.oaconvolve用法及代碼示例
- Python SciPy signal.hilbert用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.signal.sosfreqz。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
