Python SciPy signal.freqz用法及代碼示例

本文簡要介紹 python 語言中 scipy.signal.freqz 的用法。

用法:

scipy.signal.freqz(b, a=1, worN=512, whole=False, plot=None, fs=6.283185307179586, include_nyquist=False)#

計算數字濾波器的頻率響應。

給定數字濾波器的M-order 分子 b 和 N-order 分母 a，計算其頻率響應：

jw                 -jw              -jwM
   jw    B(e  )    b[0] + b[1]e    + ... + b[M]e
H(e  ) = ------ = -----------------------------------
            jw                 -jw              -jwN
         A(e  )    a[0] + a[1]e    + ... + a[N]e

參數 ：：

b： array_like

線性濾波器的分子。如果b維度大於 1，假設係數存儲在第一個維度中，並且b.shape[1:],a.shape[1:]，並且頻率陣列的形狀必須與廣播兼容。

a： array_like

線性濾波器的分母。如果b維度大於 1，假設係數存儲在第一個維度中，並且b.shape[1:],a.shape[1:]，並且頻率陣列的形狀必須與廣播兼容。

worN： {無，int，數組}，可選

如果是單個整數，則以那麽多頻率進行計算(默認為 N=512)。這是一個方便的替代方案：

np.linspace(0, fs if whole else fs/2, N, endpoint=include_nyquist)

對 FFT 計算使用快速的數字可以提高計算速度(請參閱注釋)。

如果是 數組，計算給定頻率的響應。這些與 fs 的單位相同。

whole： 布爾型，可選

通常，頻率的計算範圍是從 0 到奈奎斯特頻率 fs/2(upper-half of unit-circle)。如果整體為真，則計算從 0 到 fs 的頻率。如果 worN 是 數組，則忽略。

plot： 可調用的

帶有兩個參數的可調用對象。如果給定，返回參數w和h被傳遞給情節。用於繪製內部的頻率響應freqz.

fs： 浮點數，可選

數字係統的采樣頻率。默認為 2*pi 弧度/樣本(所以 w 是從 0 到 pi)。

include_nyquist： 布爾型，可選

如果整體為 False 且 worN 為整數，則將 include_nyquist 設置為 True 將包括最後一個頻率(奈奎斯特頻率)，否則將被忽略。

返回 ：：

w： ndarray

計算 h 的頻率，單位與 fs 相同。默認情況下，w 被歸一化為範圍 [0, pi)(弧度/樣本)。

h： ndarray

頻率響應，作為複數。

注意：

使用 Matplotlib 的matplotlib.pyplot.plot作為可調用函數陰謀產生意想不到的結果，因為這繪製了複數傳遞函數的實部，而不是幅度。嘗試lambda w, h: plot(w, np.abs(h)).

當滿足以下條件時，通過 (R)FFT 的直接計算用於計算頻率響應：

1. 給 worN 一個整數值。

2. 用過通過 FFT 計算速度很快(即，scipy.fft.next_fast_len等於用過)。

3. 分母係數是單個值(a.shape[0] == 1)。

4. 用過至少與分子係數一樣長 (worN >= b.shape[0])。

5. 如果 b.ndim > 1 ，那麽 b.shape[-1] == 1 。

對於長 FIR 濾波器，FFT 方法可以具有更低的誤差並且比等效的直接多項式計算要快得多。

例子：

>>> from scipy import signal
>>> import numpy as np
>>> b = signal.firwin(80, 0.5, window=('kaiser', 8))
>>> w, h = signal.freqz(b)

>>> import matplotlib.pyplot as plt
>>> fig, ax1 = plt.subplots()
>>> ax1.set_title('Digital filter frequency response')

>>> ax1.plot(w, 20 * np.log10(abs(h)), 'b')
>>> ax1.set_ylabel('Amplitude [dB]', color='b')
>>> ax1.set_xlabel('Frequency [rad/sample]')

>>> ax2 = ax1.twinx()
>>> angles = np.unwrap(np.angle(h))
>>> ax2.plot(w, angles, 'g')
>>> ax2.set_ylabel('Angle (radians)', color='g')
>>> ax2.grid(True)
>>> ax2.axis('tight')
>>> plt.show()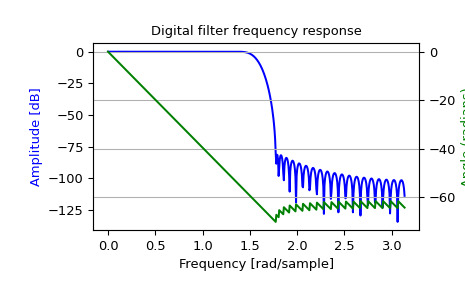

廣播示例

假設我們有兩個 FIR 濾波器，它們的係數存儲在形狀為 (2, 25) 的數組的行中。對於這個演示，我們將使用隨機數據：

>>> rng = np.random.default_rng()
>>> b = rng.random((2, 25))

要通過一次調用 freqz 來計算這兩個濾波器的頻率響應，我們必須傳入 b.T ，因為 freqz 期望第一個軸保存係數。然後，我們必須將形狀擴展為長度為 1 的簡單維度，以允許使用頻率陣列進行廣播。也就是說，我們傳入 b.T[..., np.newaxis] ，其形狀為 (25, 2, 1)：

>>> w, h = signal.freqz(b.T[..., np.newaxis], worN=1024)
>>> w.shape
(1024,)
>>> h.shape
(2, 1024)

現在，假設我們有兩個傳遞函數，具有相同的分子係數b = [0.5, 0.5].兩個分母的係數存儲在二維數組的第一維中a：

a = [   1      1  ]
    [ -0.25, -0.5 ]

>>> b = np.array([0.5, 0.5])
>>> a = np.array([[1, 1], [-0.25, -0.5]])

僅有的a大於一維。為了使其與頻率廣播兼容，我們在調用中將其擴展為一個微不足道的維度freqz：

>>> w, h = signal.freqz(b, a[..., np.newaxis], worN=1024)
>>> w.shape
(1024,)
>>> h.shape
(2, 1024)