本文簡要介紹 python 語言中 scipy.stats.boxcox 的用法。
用法:
scipy.stats.boxcox(x, lmbda=None, alpha=None, optimizer=None)#返回由Box-Cox 冪變換變換的數據集。
- x: ndarray
要轉換的輸入數組。
如果lmbda不是無,這是一個別名scipy.special.boxcox.如果返回 nan
x < 0;如果返回 -infx == 0 and lmbda < 0.如果 lmbda 為 None,則數組必須為正數、一維且非常量。
- lmbda: 標量,可選
如果 lmbda 為 None(默認),則找到使對數似然函數最大化的 lmbda 值,並將其作為第二個輸出參數返回。
如果 lmbda 不是 None,則對該值進行轉換。
- alpha: 浮點數,可選
如果lmbda是無並且scipy.stats.alpha不是 None (默認),返回
100 * (1-alpha)%置信區間lmbda作為第三個輸出參數。必須介於 0.0 和 1.0 之間。如果lmbda不是無,scipy.stats.alpha被忽略。
- optimizer: 可調用的,可選的
如果 lmbda 為 None,則優化器是用於查找使負對數似然函數最小化的 lmbda 值的標量優化器。優化器是一種接受一個參數的可調用函數:
- 樂趣 可調用的
目標函數,在給定的 lmbda 值下評估負對數似然函數
並返回一個對象,例如
scipy.optimize.OptimizeResult,它持有的最優值lmbda在一個屬性中x.有關詳細信息,請參閱
boxcox_normmax中的示例或scipy.optimize.minimize_scalar的文檔。如果 lmbda 不是 None,則忽略優化器。
- boxcox: ndarray
Box-Cox 冪變換數組。
- maxlog: 浮點數,可選
如果 lmbda 參數為 None,則第二個返回參數是最大化對數似然函數的 lmbda。
- (min_ci, max_ci): 浮點數元組,可選
如果lmbda參數為 None 並且scipy.stats.alpha不是無,這個返回的浮點元組表示給定的最小和最大置信限scipy.stats.alpha.
參數 ::
返回 ::
注意:
Box-Cox 變換由下式給出:
y = (x**lmbda - 1) / lmbda, for lmbda != 0 log(x), for lmbda = 0boxcox要求輸入數據為正數。有時,Box-Cox 轉換提供了一個移位參數來實現這一點;boxcox才不是。這樣的移位參數等價於在x調用之前boxcox.提供
alpha時返回的置信限給出以下區間:其中
llf為對數似然函數, 為卡方函數。參考:
G.E.P. Box 和 D.R.考克斯,“變革分析”,皇家統計學會雜誌 B,26, 211-252 (1964)。
例子:
>>> from scipy import stats >>> import matplotlib.pyplot as plt我們從非正態分布中生成一些隨機變量,並為它製作一個概率圖,以表明它在尾部是非正態的:
>>> fig = plt.figure() >>> ax1 = fig.add_subplot(211) >>> x = stats.loggamma.rvs(5, size=500) + 5 >>> prob = stats.probplot(x, dist=stats.norm, plot=ax1) >>> ax1.set_xlabel('') >>> ax1.set_title('Probplot against normal distribution')我們現在使用
boxcox來轉換數據,使其最接近正常:>>> ax2 = fig.add_subplot(212) >>> xt, _ = stats.boxcox(x) >>> prob = stats.probplot(xt, dist=stats.norm, plot=ax2) >>> ax2.set_title('Probplot after Box-Cox transformation')>>> plt.show()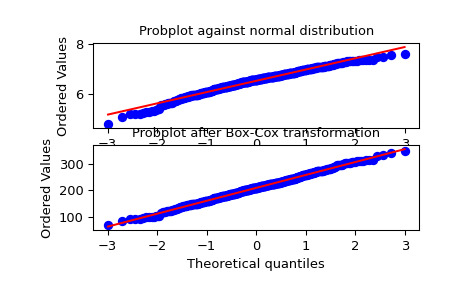
相關用法
- Python SciPy stats.boxcox_normplot用法及代碼示例
- Python SciPy stats.boxcox_normmax用法及代碼示例
- Python SciPy stats.boxcox_llf用法及代碼示例
- Python SciPy stats.boltzmann用法及代碼示例
- Python SciPy stats.boschloo_exact用法及代碼示例
- Python SciPy stats.bootstrap用法及代碼示例
- Python SciPy stats.bartlett用法及代碼示例
- Python SciPy stats.brunnermunzel用法及代碼示例
- Python SciPy stats.betaprime用法及代碼示例
- Python SciPy stats.betabinom用法及代碼示例
- Python SciPy stats.binned_statistic_2d用法及代碼示例
- Python SciPy stats.binned_statistic用法及代碼示例
- Python SciPy stats.bayes_mvs用法及代碼示例
- Python SciPy stats.burr12用法及代碼示例
- Python SciPy stats.binom用法及代碼示例
- Python SciPy stats.burr用法及代碼示例
- Python SciPy stats.bws_test用法及代碼示例
- Python SciPy stats.beta用法及代碼示例
- Python SciPy stats.bradford用法及代碼示例
- Python SciPy stats.binomtest用法及代碼示例
- Python SciPy stats.binned_statistic_dd用法及代碼示例
- Python SciPy stats.binom_test用法及代碼示例
- Python SciPy stats.bernoulli用法及代碼示例
- Python SciPy stats.barnard_exact用法及代碼示例
- Python SciPy stats.anderson用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.stats.boxcox。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
