本文簡要介紹 python 語言中 scipy.stats.binned_statistic 的用法。
用法:
scipy.stats.binned_statistic(x, values, statistic='mean', bins=10, range=None)#計算一組或多組數據的分箱統計量。
這是直方圖函數的推廣。直方圖將空間劃分為多個 bin,並返回每個 bin 中的點數。此函數允許計算每個 bin 內的值(或值集)的總和、平均值、中位數或其他統計量。
- x: (N,) 數組
要分箱的一係列值。
- values: (N,) 數組 或 (N,) 數組 列表
將根據其計算統計數據的數據。這必須與 x 具有相同的形狀,或者是一組序列 - 每個都與 x 具有相同的形狀。如果 values 是一組序列,則將獨立計算每個序列的統計量。
- statistic: 字符串或可調用,可選
要計算的統計數據(默認為‘mean’)。可用的統計數據如下:
‘mean’ : compute the mean of values for points within each bin. Empty bins will be represented by NaN.
‘std’ : compute the standard deviation within each bin. This is implicitly calculated with ddof=0.
‘median’ : compute the median of values for points within each bin. Empty bins will be represented by NaN.
‘count’ : compute the count of points within each bin. This is identical to an unweighted histogram. values array is not referenced.
‘sum’ : compute the sum of values for points within each bin. This is identical to a weighted histogram.
‘min’ : compute the minimum of values for points within each bin. Empty bins will be represented by NaN.
‘max’ : compute the maximum of values for point within each bin. Empty bins will be represented by NaN.
function : a user-defined function which takes a 1D array of values, and outputs a single numerical statistic. This function will be called on the values in each bin. Empty bins will be represented by function([]), or NaN if this returns an error.
- bins: int 或標量序列,可選
如果箱子是一個 int,它定義了給定範圍內的equal-width bin 的數量(默認為 10)。如果箱子是一個序列,它定義了 bin 邊,包括最右邊的邊,允許不均勻的 bin 寬度。值x小於最低 bin 邊的被分配給 bin 編號 0,超出最高 bin 的值被分配給
bins[-1].如果指定了 bin 邊,則 bin 的數量將為 (nx = len(bins)-1)。- range: (float, float) 或 [(float, float)], 可選
bin 的下限和上限範圍。如果未提供,範圍隻是
(x.min(), x.max())。超出範圍的值將被忽略。
- statistic: 數組
每個 bin 中所選統計數據的值。
- bin_edges: dtype 浮點數組
返回 bin 邊
(length(statistic)+1)。- binnumber:一維整數數組
x 的每個值所屬的 bin 的索引(對應於bin_edges)。與值的長度相同。 binnumber 為 i 表示對應的值介於 (bin_edges[i-1], bin_edges[i]) 之間。
參數 ::
返回 ::
注意:
除了最後一個 (righthand-most) 箱子之外的所有箱子都是半開的。換句話說,如果箱子是
[1, 2, 3, 4],那麽第一個 bin 是[1, 2)(包括1個,但不包括2個)和第二個[2, 3).然而,最後一個箱子是[3, 4], 哪一個包括 4.例子:
>>> import numpy as np >>> from scipy import stats >>> import matplotlib.pyplot as plt首先是一些基本的例子:
在給定樣本的範圍內創建兩個均勻間隔的 bin,並對每個 bin 中的相應值求和:
>>> values = [1.0, 1.0, 2.0, 1.5, 3.0] >>> stats.binned_statistic([1, 1, 2, 5, 7], values, 'sum', bins=2) BinnedStatisticResult(statistic=array([4. , 4.5]), bin_edges=array([1., 4., 7.]), binnumber=array([1, 1, 1, 2, 2]))也可以傳遞多個值數組。統計量是在每個集合上獨立計算的:
>>> values = [[1.0, 1.0, 2.0, 1.5, 3.0], [2.0, 2.0, 4.0, 3.0, 6.0]] >>> stats.binned_statistic([1, 1, 2, 5, 7], values, 'sum', bins=2) BinnedStatisticResult(statistic=array([[4. , 4.5], [8. , 9. ]]), bin_edges=array([1., 4., 7.]), binnumber=array([1, 1, 1, 2, 2]))>>> stats.binned_statistic([1, 2, 1, 2, 4], np.arange(5), statistic='mean', ... bins=3) BinnedStatisticResult(statistic=array([1., 2., 4.]), bin_edges=array([1., 2., 3., 4.]), binnumber=array([1, 2, 1, 2, 3]))作為第二個例子,我們現在生成一些作為風速函數的帆船速度的隨機數據,然後確定我們的船在特定風速下的速度:
>>> rng = np.random.default_rng() >>> windspeed = 8 * rng.random(500) >>> boatspeed = .3 * windspeed**.5 + .2 * rng.random(500) >>> bin_means, bin_edges, binnumber = stats.binned_statistic(windspeed, ... boatspeed, statistic='median', bins=[1,2,3,4,5,6,7]) >>> plt.figure() >>> plt.plot(windspeed, boatspeed, 'b.', label='raw data') >>> plt.hlines(bin_means, bin_edges[:-1], bin_edges[1:], colors='g', lw=5, ... label='binned statistic of data') >>> plt.legend()現在我們可以使用
binnumber來選擇風速低於 1 的所有數據點:>>> low_boatspeed = boatspeed[binnumber == 0]作為最後一個示例,我們將使用
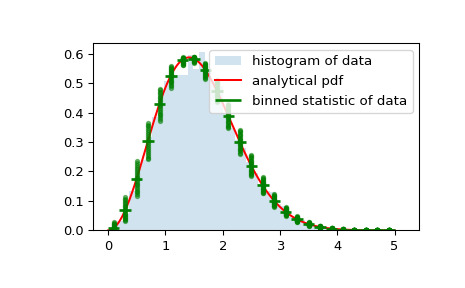
bin_edges和binnumber在常規直方圖和概率分布函數之上繪製一個分布圖,顯示每個 bin 的平均值和圍繞該平均值的分布:>>> x = np.linspace(0, 5, num=500) >>> x_pdf = stats.maxwell.pdf(x) >>> samples = stats.maxwell.rvs(size=10000)>>> bin_means, bin_edges, binnumber = stats.binned_statistic(x, x_pdf, ... statistic='mean', bins=25) >>> bin_width = (bin_edges[1] - bin_edges[0]) >>> bin_centers = bin_edges[1:] - bin_width/2>>> plt.figure() >>> plt.hist(samples, bins=50, density=True, histtype='stepfilled', ... alpha=0.2, label='histogram of data') >>> plt.plot(x, x_pdf, 'r-', label='analytical pdf') >>> plt.hlines(bin_means, bin_edges[:-1], bin_edges[1:], colors='g', lw=2, ... label='binned statistic of data') >>> plt.plot((binnumber - 0.5) * bin_width, x_pdf, 'g.', alpha=0.5) >>> plt.legend(fontsize=10) >>> plt.show()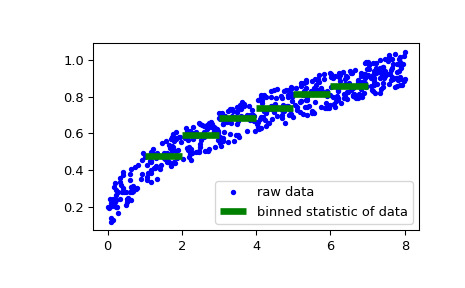
相關用法
- Python SciPy stats.binned_statistic_2d用法及代碼示例
- Python SciPy stats.binned_statistic_dd用法及代碼示例
- Python SciPy stats.binom用法及代碼示例
- Python SciPy stats.binomtest用法及代碼示例
- Python SciPy stats.binom_test用法及代碼示例
- Python SciPy stats.bartlett用法及代碼示例
- Python SciPy stats.boltzmann用法及代碼示例
- Python SciPy stats.brunnermunzel用法及代碼示例
- Python SciPy stats.betaprime用法及代碼示例
- Python SciPy stats.betabinom用法及代碼示例
- Python SciPy stats.boxcox_normplot用法及代碼示例
- Python SciPy stats.boxcox用法及代碼示例
- Python SciPy stats.bayes_mvs用法及代碼示例
- Python SciPy stats.boxcox_normmax用法及代碼示例
- Python SciPy stats.burr12用法及代碼示例
- Python SciPy stats.boschloo_exact用法及代碼示例
- Python SciPy stats.bootstrap用法及代碼示例
- Python SciPy stats.burr用法及代碼示例
- Python SciPy stats.bws_test用法及代碼示例
- Python SciPy stats.beta用法及代碼示例
- Python SciPy stats.bradford用法及代碼示例
- Python SciPy stats.boxcox_llf用法及代碼示例
- Python SciPy stats.bernoulli用法及代碼示例
- Python SciPy stats.barnard_exact用法及代碼示例
- Python SciPy stats.anderson用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.stats.binned_statistic。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
