Python SciPy stats.bootstrap用法及代碼示例

本文簡要介紹 python 語言中 scipy.stats.bootstrap 的用法。

用法:

scipy.stats.bootstrap(data, statistic, *, n_resamples=9999, batch=None, vectorized=None, paired=False, axis=0, confidence_level=0.95, alternative='two-sided', method='BCa', bootstrap_result=None, random_state=None)#

計算統計量的兩側引導置信區間。

什麽時候方法是'percentile'和選擇是'two-sided'，根據以下過程計算自舉置信區間。

1. 對數據重新采樣：對於data中的每個樣本和n_resamples中的每一個，隨機抽取與原始樣本大小相同的原始樣本(有放回)。

2. 計算統計量的引導分布：對於每組重采樣，計算檢驗統計量。

3. 確定置信區間：找到自舉分布的區間，即

   • 對稱於中位數和

   • 包含confidence_level 個重采樣統計值。

雖然 'percentile' 方法最直觀，但在實踐中很少使用。有兩種更常見的方法可用，'basic'(“反向百分位數”)和'BCa'(“偏差校正和加速”)；它們的不同之處在於步驟 3 的執行方式。

如果樣本在數據從它們各自的分布中隨機抽取\(n\)次，置信區間返回bootstrap將包含這些分布的統計數據的真實值confidence_level\(\, \times \, n\)次。

參數 ：：

data： 類似數組的序列

每個數據元素都是來自底層分布的樣本。

statistic： 可調用的

要計算置信區間的統計量。統計必須是接受的可調用對象len(data)樣本作為單獨的參數並返回結果統計信息。如果矢量化已設置True,統計還必須接受關鍵字參數軸並被矢量化以計算沿提供的統計量軸.

n_resamples： 整數，默認值：9999

為形成統計量的自舉分布而執行的重采樣次數。

batch： 整數，可選

在每個向量化調用中要處理的重采樣數統計.內存使用量為 O(批*n)， 在哪裏n是樣本量。默認為None， 在這種情況下batch = n_resamples(或者batch = max(n_resamples, n)為了method='BCa')。

vectorized： 布爾型，可選

如果矢量化已設置False,統計不會傳遞關鍵字參數軸並且預計僅計算一維樣本的統計量。如果True,統計將傳遞關鍵字參數軸並預計將計算統計數據軸當傳遞 ND 樣本數組時。如果None(默認)，矢量化將被設置True如果axis是一個參數統計。使用矢量化統計通常可以減少計算時間。

paired： 布爾值，默認值：False

統計數據是否將數據中樣本的對應元素視為配對。

axis： 整數，默認值：0

沿其計算統計量的數據中樣本的軸。

confidence_level： 浮點數，默認：0.95

置信區間的置信水平。

alternative： {‘雙麵’,‘less’, ‘greater’}，默認：'two-sided'

選擇'two-sided'(默認)對於雙邊置信區間，'less'對於單邊置信區間，下限為-np.inf， 和'greater'對於單邊置信區間，其上限為np.inf。單邊置信區間的另一個界限與雙邊置信區間的相同confidence_level距離 1.0 相差兩倍；例如95% 的上限'less'置信區間與 90% 的上限相同'two-sided'置信區間。

method： {‘percentile’, ‘basic’, ‘bca’}，默認：'BCa'

是否返回 ‘percentile’ 引導置信區間 ( 'percentile' )、‘basic’ (AKA ‘reverse’) 引導置信區間 ( 'basic' ) 或偏差校正和加速引導置信區間 ( 'BCa' ) 。

bootstrap_result： BootstrapResult，可選

提供先前調用返回的結果對象bootstrap將以前的 bootstrap 發行版包含在新的 bootstrap 發行版中。例如，這可以用來改變confidence_level， 改變方法，或者查看執行額外重采樣而不重複計算的效果。

random_state： {無，整數， numpy.random.Generator ，

numpy.random.RandomState}, optional

用於生成重采樣的偽隨機數生成器狀態。

如果random_state是None(或者np.random)， 這numpy.random.RandomState使用單例。如果random_state是一個 int，一個新的RandomState使用實例，播種random_state.如果random_state已經是一個Generator或者RandomState實例然後使用該實例。

返回 ：：

res： BootstrapResult

具有屬性的對象：

confidence_interval ConfidenceInterval

引導置信區間作為一個實例collections.namedtuple有屬性低的和高的.

bootstrap_distribution ndarray

自舉分布，即統計對於每次重新采樣。最後一個維度與重新采樣相對應(例如res.bootstrap_distribution.shape[-1] == n_resamples)。

standard_error 浮點數或 ndarray

Bootstrap 標準誤，即 Bootstrap 分布的樣本標準差。

警告 ：：

DegenerateDataWarning

當 method='BCa' 且引導分布退化時生成(例如，所有元素都相同)。

注意：

置信區間的元素可能是NaNmethod='BCa'如果引導分布是退化的(例如所有元素都是相同的)。在這種情況下，考慮使用另一個方法或檢查數據以表明其他分析可能更合適(例如，所有觀察結果都是相同的)。

參考：

[1]

B. Efron 和 R. J. Tibshirani，Bootstrap 簡介，Chapman & Hall/CRC，博卡拉頓，佛羅裏達州，美國(1993 年)

[2]

Nathaniel E. Helwig，“Bootstrap Confidence Intervals”，http://users.stat.umn.edu/~helwig/notes/bootci-Notes.pdf

[3]

自舉(統計)，維基百科，https://en.wikipedia.org/wiki/Bootstrapping_%28statistics%29

例子：

假設我們從未知分布中采樣數據。

>>> import numpy as np
>>> rng = np.random.default_rng()
>>> from scipy.stats import norm
>>> dist = norm(loc=2, scale=4)  # our "unknown" distribution
>>> data = dist.rvs(size=100, random_state=rng)

我們對分布的標準差感興趣。

>>> std_true = dist.std()      # the true value of the statistic
>>> print(std_true)
4.0
>>> std_sample = np.std(data)  # the sample statistic
>>> print(std_sample)
3.9460644295563863

如果我們要從未知分布中重複采樣並每次計算樣本的統計量，則引導程序用於近似我們期望的變異性。它通過替換地重複對原始樣本的值進行重采樣並計算每個重采樣的統計量來實現此目的。這會產生“bootstrap distribution” 統計數據。

>>> import matplotlib.pyplot as plt
>>> from scipy.stats import bootstrap
>>> data = (data,)  # samples must be in a sequence
>>> res = bootstrap(data, np.std, confidence_level=0.9,
...                 random_state=rng)
>>> fig, ax = plt.subplots()
>>> ax.hist(res.bootstrap_distribution, bins=25)
>>> ax.set_title('Bootstrap Distribution')
>>> ax.set_xlabel('statistic value')
>>> ax.set_ylabel('frequency')
>>> plt.show()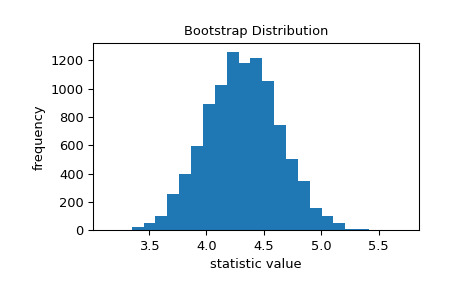

標準誤差量化了這種變異性。它被計算為引導分布的標準差。

>>> res.standard_error
0.24427002125829136
>>> res.standard_error == np.std(res.bootstrap_distribution, ddof=1)
True

統計量的自舉分布通常近似正態，其尺度等於標準誤差。

>>> x = np.linspace(3, 5)
>>> pdf = norm.pdf(x, loc=std_sample, scale=res.standard_error)
>>> fig, ax = plt.subplots()
>>> ax.hist(res.bootstrap_distribution, bins=25, density=True)
>>> ax.plot(x, pdf)
>>> ax.set_title('Normal Approximation of the Bootstrap Distribution')
>>> ax.set_xlabel('statistic value')
>>> ax.set_ylabel('pdf')
>>> plt.show()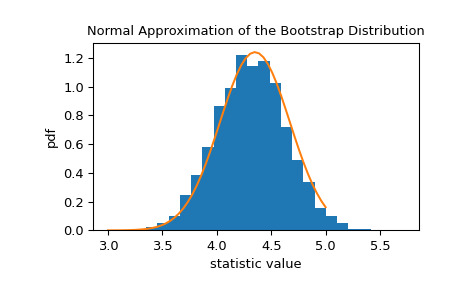

這表明我們可以根據該正態分布的分位數構建統計量的 90% 置信區間。

>>> norm.interval(0.9, loc=std_sample, scale=res.standard_error)
(3.5442759991341726, 4.3478528599786)

由於中心極限定理，這種正態近似對於樣本背後的各種統計數據和分布都是準確的；然而，該近似值並非在所有情況下都可靠。由於 bootstrap 旨在處理任意基礎分布和統計數據，因此它使用更先進的技術來生成準確的置信區間。

>>> print(res.confidence_interval)
ConfidenceInterval(low=3.57655333533867, high=4.382043696342881)

如果我們從原始分布中采樣 1000 次並為每個樣本形成引導置信區間，則置信區間大約 90% 的時間包含統計量的真實值。

>>> n_trials = 1000
>>> ci_contains_true_std = 0
>>> for i in range(n_trials):
...    data = (dist.rvs(size=100, random_state=rng),)
...    ci = bootstrap(data, np.std, confidence_level=0.9, n_resamples=1000,
...                   random_state=rng).confidence_interval
...    if ci[0] < std_true < ci[1]:
...        ci_contains_true_std += 1
>>> print(ci_contains_true_std)
875

除了編寫循環之外，我們還可以一次確定所有 1000 個樣本的置信區間。

>>> data = (dist.rvs(size=(n_trials, 100), random_state=rng),)
>>> res = bootstrap(data, np.std, axis=-1, confidence_level=0.9,
...                 n_resamples=1000, random_state=rng)
>>> ci_l, ci_u = res.confidence_interval

這裏，ci_l和ci_u包含每個的置信區間n_trials = 1000樣品。

>>> print(ci_l[995:])
[3.77729695 3.75090233 3.45829131 3.34078217 3.48072829]
>>> print(ci_u[995:])
[4.88316666 4.86924034 4.32032996 4.2822427  4.59360598]

同樣，大約 90% 包含真實值 std_true = 4 。

>>> print(np.sum((ci_l < std_true) & (std_true < ci_u)))
900

bootstrap也可用於估計多樣本統計的置信區間，包括通過假設檢驗計算的置信區間。scipy.stats.mood執行等尺度參數的 Mood 檢驗，它返回兩個輸出：統計量和 p 值。為了獲得檢驗統計量的置信區間，我們首先換行scipy.stats.mood在接受兩個樣本參數的函數中，接受一個軸關鍵字參數，並僅返回統計信息。

>>> from scipy.stats import mood
>>> def my_statistic(sample1, sample2, axis):
...     statistic, _ = mood(sample1, sample2, axis=-1)
...     return statistic

在這裏，我們使用具有默認 95% 置信水平的 ‘percentile’ 方法。

>>> sample1 = norm.rvs(scale=1, size=100, random_state=rng)
>>> sample2 = norm.rvs(scale=2, size=100, random_state=rng)
>>> data = (sample1, sample2)
>>> res = bootstrap(data, my_statistic, method='basic', random_state=rng)
>>> print(mood(sample1, sample2)[0])  # element 0 is the statistic
-5.521109549096542
>>> print(res.confidence_interval)
ConfidenceInterval(low=-7.255994487314675, high=-4.016202624747605)

標準誤差的 bootstrap 估計也是可用的。

>>> print(res.standard_error)
0.8344963846318795

配對樣本統計也有效。例如，考慮 Pearson 相關係數。

>>> from scipy.stats import pearsonr
>>> n = 100
>>> x = np.linspace(0, 10, n)
>>> y = x + rng.uniform(size=n)
>>> print(pearsonr(x, y)[0])  # element 0 is the statistic
0.9962357936065914

我們包裝 pearsonr 以便它隻返回統計信息。

>>> def my_statistic(x, y):
...     return pearsonr(x, y)[0]

我們使用 paired=True 調用 bootstrap 。此外，由於 my_statistic 未進行矢量化以計算沿給定軸的統計量，因此我們傳入 vectorized=False 。

>>> res = bootstrap((x, y), my_statistic, vectorized=False, paired=True,
...                 random_state=rng)
>>> print(res.confidence_interval)
ConfidenceInterval(low=0.9950085825848624, high=0.9971212407917498)

結果對象可以傳回到bootstrap以執行額外的重采樣：

>>> len(res.bootstrap_distribution)
9999
>>> res = bootstrap((x, y), my_statistic, vectorized=False, paired=True,
...                 n_resamples=1001, random_state=rng,
...                 bootstrap_result=res)
>>> len(res.bootstrap_distribution)
11000

或更改置信區間選項：

>>> res2 = bootstrap((x, y), my_statistic, vectorized=False, paired=True,
...                  n_resamples=0, random_state=rng, bootstrap_result=res,
...                  method='percentile', confidence_level=0.9)
>>> np.testing.assert_equal(res2.bootstrap_distribution,
...                         res.bootstrap_distribution)
>>> res.confidence_interval
ConfidenceInterval(low=0.9950035351407804, high=0.9971170323404578)

無需重複計算原始引導分布。