本文簡要介紹 python 語言中 scipy.interpolate.SmoothSphereBivariateSpline 的用法。
用法:
class scipy.interpolate.SmoothSphereBivariateSpline(theta, phi, r, w=None, s=0.0, eps=1e-16)#球坐標中的平滑二元樣條近似。
- theta, phi, r: array_like
一維數據點序列(順序不重要)。坐標必須以弧度表示。 Theta 必須位於區間
[0, pi]內,而 phi 必須位於區間[0, 2pi]內。- w: 數組,可選
正的一維權重序列。
- s: 浮點數,可選
為估計條件定義的正平滑因子:
sum((w(i)*(r(i) - s(theta(i), phi(i))))**2, axis=0) <= s默認s=len(w)如果1/w[i]是對r[i]的標準偏差的估計,則該值應該是一個不錯的值。- eps: 浮點數,可選
用於確定over-determined 線性方程組的有效等級的閾值。每股收益應該在開區間內有一個值
(0, 1),默認為 1e-16。
參數 ::
注意:
有關詳細信息,請參閱有關此函數的FITPACK 站點。
例子:
假設我們在粗網格上有全局數據(輸入數據不必在網格上):
>>> import numpy as np >>> theta = np.linspace(0., np.pi, 7) >>> phi = np.linspace(0., 2*np.pi, 9) >>> data = np.empty((theta.shape[0], phi.shape[0])) >>> data[:,0], data[0,:], data[-1,:] = 0., 0., 0. >>> data[1:-1,1], data[1:-1,-1] = 1., 1. >>> data[1,1:-1], data[-2,1:-1] = 1., 1. >>> data[2:-2,2], data[2:-2,-2] = 2., 2. >>> data[2,2:-2], data[-3,2:-2] = 2., 2. >>> data[3,3:-2] = 3. >>> data = np.roll(data, 4, 1)我們需要設置插值器對象
>>> lats, lons = np.meshgrid(theta, phi) >>> from scipy.interpolate import SmoothSphereBivariateSpline >>> lut = SmoothSphereBivariateSpline(lats.ravel(), lons.ravel(), ... data.T.ravel(), s=3.5)作為第一個測試,我們將看到算法在輸入坐標上運行時返回什麽
>>> data_orig = lut(theta, phi)最後,我們將數據插入到更精細的網格中
>>> fine_lats = np.linspace(0., np.pi, 70) >>> fine_lons = np.linspace(0., 2 * np.pi, 90)>>> data_smth = lut(fine_lats, fine_lons)>>> import matplotlib.pyplot as plt >>> fig = plt.figure() >>> ax1 = fig.add_subplot(131) >>> ax1.imshow(data, interpolation='nearest') >>> ax2 = fig.add_subplot(132) >>> ax2.imshow(data_orig, interpolation='nearest') >>> ax3 = fig.add_subplot(133) >>> ax3.imshow(data_smth, interpolation='nearest') >>> plt.show()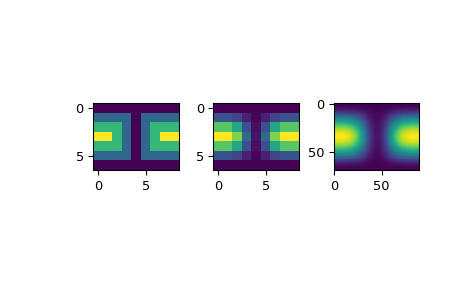
相關用法
- Python SciPy interpolate.make_interp_spline用法及代碼示例
- Python SciPy interpolate.krogh_interpolate用法及代碼示例
- Python SciPy interpolate.InterpolatedUnivariateSpline用法及代碼示例
- Python SciPy interpolate.BSpline用法及代碼示例
- Python SciPy interpolate.LSQSphereBivariateSpline用法及代碼示例
- Python SciPy interpolate.griddata用法及代碼示例
- Python SciPy interpolate.splder用法及代碼示例
- Python SciPy interpolate.LinearNDInterpolator用法及代碼示例
- Python SciPy interpolate.PPoly用法及代碼示例
- Python SciPy interpolate.NdBSpline用法及代碼示例
- Python SciPy interpolate.pade用法及代碼示例
- Python SciPy interpolate.barycentric_interpolate用法及代碼示例
- Python SciPy interpolate.RegularGridInterpolator用法及代碼示例
- Python SciPy interpolate.NdPPoly用法及代碼示例
- Python SciPy interpolate.interp2d用法及代碼示例
- Python SciPy interpolate.approximate_taylor_polynomial用法及代碼示例
- Python SciPy interpolate.RectSphereBivariateSpline用法及代碼示例
- Python SciPy interpolate.sproot用法及代碼示例
- Python SciPy interpolate.splantider用法及代碼示例
- Python SciPy interpolate.CloughTocher2DInterpolator用法及代碼示例
- Python SciPy interpolate.interp1d用法及代碼示例
- Python SciPy interpolate.BPoly用法及代碼示例
- Python SciPy interpolate.BarycentricInterpolator用法及代碼示例
- Python SciPy interpolate.splrep用法及代碼示例
- Python SciPy interpolate.make_smoothing_spline用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.interpolate.SmoothSphereBivariateSpline。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
