本文简要介绍 python 语言中 scipy.stats.yeojohnson_llf 的用法。
用法:
scipy.stats.yeojohnson_llf(lmb, data)#yeojohnson 对数似然函数。
- lmb: 标量
Yeo-Johnson 转换的参数。有关详细信息,请参阅
yeojohnson。- data: array_like
用于计算 Yeo-Johnson 对数似然的数据。如果数据是多维的,则沿第一个轴计算对数似然。
- llf: 浮点数
Yeo-Johnson 给定 lmb 的数据的对数似然。
参数 ::
返回 ::
注意:
Yeo-Johnson 对数似然函数在这里定义为
其中 是 Yeo-Johnson 变换后的输入数据
x的估计方差。例子:
>>> import numpy as np >>> from scipy import stats >>> import matplotlib.pyplot as plt >>> from mpl_toolkits.axes_grid1.inset_locator import inset_axes生成一些随机变量并计算
lmbda值范围内的Yeo-Johnson 对数似然值:>>> x = stats.loggamma.rvs(5, loc=10, size=1000) >>> lmbdas = np.linspace(-2, 10) >>> llf = np.zeros(lmbdas.shape, dtype=float) >>> for ii, lmbda in enumerate(lmbdas): ... llf[ii] = stats.yeojohnson_llf(lmbda, x)还可以使用
yeojohnson找到最佳 lmbda 值:>>> x_most_normal, lmbda_optimal = stats.yeojohnson(x)将对数似然绘制为 lmbda 的函数。将最佳 lmbda 添加为水平线,以检查这是否确实是最佳值:
>>> fig = plt.figure() >>> ax = fig.add_subplot(111) >>> ax.plot(lmbdas, llf, 'b.-') >>> ax.axhline(stats.yeojohnson_llf(lmbda_optimal, x), color='r') >>> ax.set_xlabel('lmbda parameter') >>> ax.set_ylabel('Yeo-Johnson log-likelihood')现在添加一些概率图,以显示在对数似然最大化的情况下,使用
yeojohnson转换的数据看起来最接近正常:>>> locs = [3, 10, 4] # 'lower left', 'center', 'lower right' >>> for lmbda, loc in zip([-1, lmbda_optimal, 9], locs): ... xt = stats.yeojohnson(x, lmbda=lmbda) ... (osm, osr), (slope, intercept, r_sq) = stats.probplot(xt) ... ax_inset = inset_axes(ax, width="20%", height="20%", loc=loc) ... ax_inset.plot(osm, osr, 'c.', osm, slope*osm + intercept, 'k-') ... ax_inset.set_xticklabels([]) ... ax_inset.set_yticklabels([]) ... ax_inset.set_title(r'$\lambda=%1.2f$' % lmbda)>>> plt.show()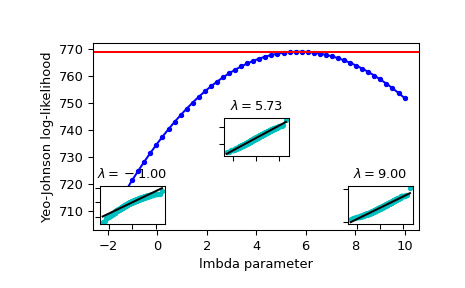
相关用法
- Python SciPy stats.yeojohnson_normmax用法及代码示例
- Python SciPy stats.yeojohnson_normplot用法及代码示例
- Python SciPy stats.yeojohnson用法及代码示例
- Python SciPy stats.yulesimon用法及代码示例
- Python SciPy stats.anderson用法及代码示例
- Python SciPy stats.iqr用法及代码示例
- Python SciPy stats.genpareto用法及代码示例
- Python SciPy stats.skewnorm用法及代码示例
- Python SciPy stats.cosine用法及代码示例
- Python SciPy stats.norminvgauss用法及代码示例
- Python SciPy stats.directional_stats用法及代码示例
- Python SciPy stats.invwishart用法及代码示例
- Python SciPy stats.bartlett用法及代码示例
- Python SciPy stats.levy_stable用法及代码示例
- Python SciPy stats.page_trend_test用法及代码示例
- Python SciPy stats.itemfreq用法及代码示例
- Python SciPy stats.exponpow用法及代码示例
- Python SciPy stats.gumbel_l用法及代码示例
- Python SciPy stats.chisquare用法及代码示例
- Python SciPy stats.semicircular用法及代码示例
- Python SciPy stats.gzscore用法及代码示例
- Python SciPy stats.gompertz用法及代码示例
- Python SciPy stats.normaltest用法及代码示例
- Python SciPy stats.dirichlet_multinomial用法及代码示例
- Python SciPy stats.genlogistic用法及代码示例
注:本文由纯净天空筛选整理自scipy.org大神的英文原创作品 scipy.stats.yeojohnson_llf。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
