本文简要介绍 python 语言中 scipy.stats.yeojohnson 的用法。
用法:
scipy.stats.yeojohnson(x, lmbda=None)#返回由Yeo-Johnson 幂变换变换的数据集。
- x: ndarray
输入数组。应该是一维的。
- lmbda: 浮点数,可选
如果
lmbda是None,找到最大化对数似然函数的 lambda 并将其作为第二个输出参数返回。否则,将对给定值进行转换。
- 约约翰逊:ndarray
Yeo-Johnson 幂变换数组。
- maxlog: 浮点数,可选
如果 lmbda 参数为 None,则第二个返回参数是最大化对数似然函数的 lambda。
参数 ::
返回 ::
注意:
Yeo-Johnson 变换由下式给出:
y = ((x + 1)**lmbda - 1) / lmbda, for x >= 0, lmbda != 0 log(x + 1), for x >= 0, lmbda = 0 -((-x + 1)**(2 - lmbda) - 1) / (2 - lmbda), for x < 0, lmbda != 2 -log(-x + 1), for x < 0, lmbda = 2与
boxcox不同,yeojohnson不要求输入数据为正。参考:
I. Yeo 和 R.A. Johnson,“用于改善常态或对称性的新型电源转换系列”,Biometrika 87.4 (2000):
例子:
>>> from scipy import stats >>> import matplotlib.pyplot as plt我们从非正态分布中生成一些随机变量,并为它制作一个概率图,以表明它在尾部是非正态的:
>>> fig = plt.figure() >>> ax1 = fig.add_subplot(211) >>> x = stats.loggamma.rvs(5, size=500) + 5 >>> prob = stats.probplot(x, dist=stats.norm, plot=ax1) >>> ax1.set_xlabel('') >>> ax1.set_title('Probplot against normal distribution')我们现在使用
yeojohnson来转换数据,使其最接近正常:>>> ax2 = fig.add_subplot(212) >>> xt, lmbda = stats.yeojohnson(x) >>> prob = stats.probplot(xt, dist=stats.norm, plot=ax2) >>> ax2.set_title('Probplot after Yeo-Johnson transformation')>>> plt.show()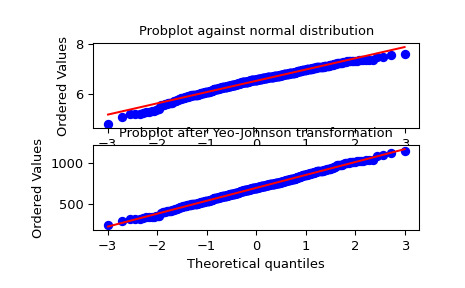
相关用法
- Python SciPy stats.yeojohnson_normmax用法及代码示例
- Python SciPy stats.yeojohnson_llf用法及代码示例
- Python SciPy stats.yeojohnson_normplot用法及代码示例
- Python SciPy stats.yulesimon用法及代码示例
- Python SciPy stats.anderson用法及代码示例
- Python SciPy stats.iqr用法及代码示例
- Python SciPy stats.genpareto用法及代码示例
- Python SciPy stats.skewnorm用法及代码示例
- Python SciPy stats.cosine用法及代码示例
- Python SciPy stats.norminvgauss用法及代码示例
- Python SciPy stats.directional_stats用法及代码示例
- Python SciPy stats.invwishart用法及代码示例
- Python SciPy stats.bartlett用法及代码示例
- Python SciPy stats.levy_stable用法及代码示例
- Python SciPy stats.page_trend_test用法及代码示例
- Python SciPy stats.itemfreq用法及代码示例
- Python SciPy stats.exponpow用法及代码示例
- Python SciPy stats.gumbel_l用法及代码示例
- Python SciPy stats.chisquare用法及代码示例
- Python SciPy stats.semicircular用法及代码示例
- Python SciPy stats.gzscore用法及代码示例
- Python SciPy stats.gompertz用法及代码示例
- Python SciPy stats.normaltest用法及代码示例
- Python SciPy stats.dirichlet_multinomial用法及代码示例
- Python SciPy stats.genlogistic用法及代码示例
注:本文由纯净天空筛选整理自scipy.org大神的英文原创作品 scipy.stats.yeojohnson。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
