本文简要介绍 python 语言中 scipy.spatial.geometric_slerp 的用法。
用法:
scipy.spatial.geometric_slerp(start, end, t, tol=1e-07)#几何球面线性插值。
插值沿任意维度空间中的unit-radius 大圆弧进行。
- start: (n_dimensions, ) 类似数组
一维数组对象中的单个 n 维输入坐标。 n 必须大于 1。
- end: (n_dimensions, ) 类似数组
一维数组对象中的单个 n 维输入坐标。 n 必须大于 1。
- t: float 或 (n_points,) 类似一维数组
表示插值参数的浮点或一维双精度数组,其值需要在 0 和 1 之间的包含区间内。常见的方法是使用
np.linspace(0, 1, n_pts)为线性间隔点生成数组。允许升序、降序和乱序。- tol: 浮点数
确定开始和结束坐标是否为对映点的绝对容差。
- result: (t.size, D)
包含插值球面路径的双精度数组,包括使用 0 和 1 t 时的开始和结束。插值应对应于 t 数组中提供的相同排序顺序。如果
t是浮点数,则结果可能是一维的。
- ValueError
如果
start和end是对映体,不在单元n-sphere上,或者针对各种退化情况。
参数 ::
返回 ::
抛出 ::
注意:
该实现基于 [1] 中提供的数学公式,并且该算法的第一个已知介绍源自对 4-D 几何的研究,在 Ken Shoemake 的原始四元数 Slerp 出版物的脚注中归功于 Glenn Davis [ 2]。
参考:
[2]Ken Shoemake (1985) 使用四元数曲线动画旋转。 ACM SIGGRAPH 计算机图形学,19(3):245-254。
例子:
在跨越 90 度的圆的圆周上插入四个 linearly-spaced 值:
>>> import numpy as np >>> from scipy.spatial import geometric_slerp >>> import matplotlib.pyplot as plt >>> fig = plt.figure() >>> ax = fig.add_subplot(111) >>> start = np.array([1, 0]) >>> end = np.array([0, 1]) >>> t_vals = np.linspace(0, 1, 4) >>> result = geometric_slerp(start, ... end, ... t_vals)插值结果应在单位圆上可识别的 30 度间隔:
>>> ax.scatter(result[...,0], result[...,1], c='k') >>> circle = plt.Circle((0, 0), 1, color='grey') >>> ax.add_artist(circle) >>> ax.set_aspect('equal') >>> plt.show()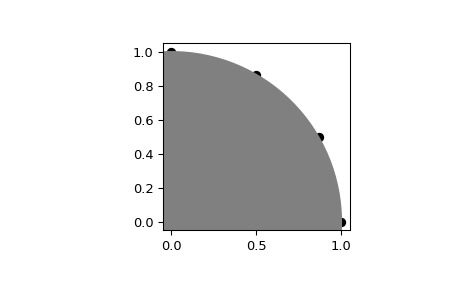
尝试在圆上的对映点之间进行插值是不明确的,因为有两条可能的路径,而在球体上,测地线表面上有无限可能的路径。尽管如此,其中一条模棱两可的路径与警告一起返回:
>>> opposite_pole = np.array([-1, 0]) >>> with np.testing.suppress_warnings() as sup: ... sup.filter(UserWarning) ... geometric_slerp(start, ... opposite_pole, ... t_vals) array([[ 1.00000000e+00, 0.00000000e+00], [ 5.00000000e-01, 8.66025404e-01], [-5.00000000e-01, 8.66025404e-01], [-1.00000000e+00, 1.22464680e-16]])将原始示例扩展到球体并绘制 3D 插值点:
>>> from mpl_toolkits.mplot3d import proj3d >>> fig = plt.figure() >>> ax = fig.add_subplot(111, projection='3d')绘制单位球以供参考(可选):
>>> u = np.linspace(0, 2 * np.pi, 100) >>> v = np.linspace(0, np.pi, 100) >>> x = np.outer(np.cos(u), np.sin(v)) >>> y = np.outer(np.sin(u), np.sin(v)) >>> z = np.outer(np.ones(np.size(u)), np.cos(v)) >>> ax.plot_surface(x, y, z, color='y', alpha=0.1)对大量点进行插值可能会在球体表面上提供平滑曲线的外观,这对于球体表面上的离散积分计算也很有用:
>>> start = np.array([1, 0, 0]) >>> end = np.array([0, 0, 1]) >>> t_vals = np.linspace(0, 1, 200) >>> result = geometric_slerp(start, ... end, ... t_vals) >>> ax.plot(result[...,0], ... result[...,1], ... result[...,2], ... c='k') >>> plt.show()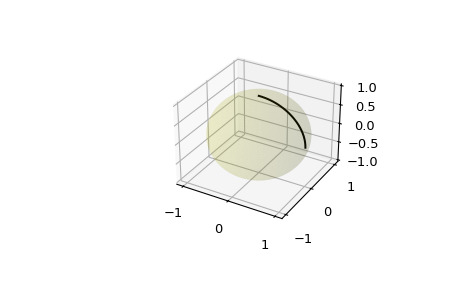
相关用法
- Python SciPy spatial.tsearch用法及代码示例
- Python SciPy spatial.Voronoi用法及代码示例
- Python SciPy spatial.procrustes用法及代码示例
- Python SciPy spatial.SphericalVoronoi用法及代码示例
- Python SciPy spatial.minkowski_distance用法及代码示例
- Python SciPy spatial.HalfspaceIntersection用法及代码示例
- Python SciPy spatial.voronoi_plot_2d用法及代码示例
- Python SciPy spatial.minkowski_distance_p用法及代码示例
- Python SciPy spatial.distance_matrix用法及代码示例
- Python SciPy spatial.ConvexHull用法及代码示例
- Python SciPy spatial.convex_hull_plot_2d用法及代码示例
- Python SciPy spatial.Delaunay用法及代码示例
- Python SciPy spatial.delaunay_plot_2d用法及代码示例
- Python SciPy sparse.isspmatrix用法及代码示例
- Python SciPy sparse.save_npz用法及代码示例
- Python SciPy sparse.issparse用法及代码示例
- Python SciPy sparse.coo_matrix用法及代码示例
- Python SciPy sparse.isspmatrix_csc用法及代码示例
- Python SciPy sparse.isspmatrix_csr用法及代码示例
- Python SciPy sparse.tril用法及代码示例
- Python SciPy sparse.coo_array用法及代码示例
- Python SciPy sparse.dia_array用法及代码示例
- Python SciPy sparse.bmat用法及代码示例
- Python SciPy sparse.hstack用法及代码示例
- Python SciPy sparse.rand用法及代码示例
注:本文由纯净天空筛选整理自scipy.org大神的英文原创作品 scipy.spatial.geometric_slerp。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
