本文簡要介紹 python 語言中 scipy.spatial.geometric_slerp 的用法。
用法:
scipy.spatial.geometric_slerp(start, end, t, tol=1e-07)#幾何球麵線性插值。
插值沿任意維度空間中的unit-radius 大圓弧進行。
- start: (n_dimensions, ) 類似數組
一維數組對象中的單個 n 維輸入坐標。 n 必須大於 1。
- end: (n_dimensions, ) 類似數組
一維數組對象中的單個 n 維輸入坐標。 n 必須大於 1。
- t: float 或 (n_points,) 類似一維數組
表示插值參數的浮點或一維雙精度數組,其值需要在 0 和 1 之間的包含區間內。常見的方法是使用
np.linspace(0, 1, n_pts)為線性間隔點生成數組。允許升序、降序和亂序。- tol: 浮點數
確定開始和結束坐標是否為對映點的絕對容差。
- result: (t.size, D)
包含插值球麵路徑的雙精度數組,包括使用 0 和 1 t 時的開始和結束。插值應對應於 t 數組中提供的相同排序順序。如果
t是浮點數,則結果可能是一維的。
- ValueError
如果
start和end是對映體,不在單元n-sphere上,或者針對各種退化情況。
參數 ::
返回 ::
拋出 ::
注意:
該實現基於 [1] 中提供的數學公式,並且該算法的第一個已知介紹源自對 4-D 幾何的研究,在 Ken Shoemake 的原始四元數 Slerp 出版物的腳注中歸功於 Glenn Davis [ 2]。
參考:
[2]Ken Shoemake (1985) 使用四元數曲線動畫旋轉。 ACM SIGGRAPH 計算機圖形學,19(3):245-254。
例子:
在跨越 90 度的圓的圓周上插入四個 linearly-spaced 值:
>>> import numpy as np >>> from scipy.spatial import geometric_slerp >>> import matplotlib.pyplot as plt >>> fig = plt.figure() >>> ax = fig.add_subplot(111) >>> start = np.array([1, 0]) >>> end = np.array([0, 1]) >>> t_vals = np.linspace(0, 1, 4) >>> result = geometric_slerp(start, ... end, ... t_vals)插值結果應在單位圓上可識別的 30 度間隔:
>>> ax.scatter(result[...,0], result[...,1], c='k') >>> circle = plt.Circle((0, 0), 1, color='grey') >>> ax.add_artist(circle) >>> ax.set_aspect('equal') >>> plt.show()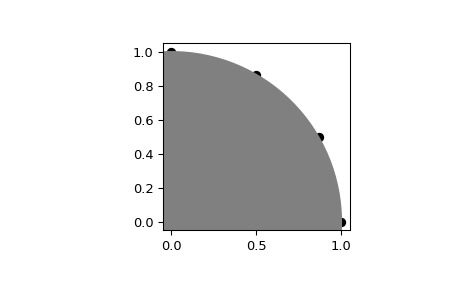
嘗試在圓上的對映點之間進行插值是不明確的,因為有兩條可能的路徑,而在球體上,測地線表麵上有無限可能的路徑。盡管如此,其中一條模棱兩可的路徑與警告一起返回:
>>> opposite_pole = np.array([-1, 0]) >>> with np.testing.suppress_warnings() as sup: ... sup.filter(UserWarning) ... geometric_slerp(start, ... opposite_pole, ... t_vals) array([[ 1.00000000e+00, 0.00000000e+00], [ 5.00000000e-01, 8.66025404e-01], [-5.00000000e-01, 8.66025404e-01], [-1.00000000e+00, 1.22464680e-16]])將原始示例擴展到球體並繪製 3D 插值點:
>>> from mpl_toolkits.mplot3d import proj3d >>> fig = plt.figure() >>> ax = fig.add_subplot(111, projection='3d')繪製單位球以供參考(可選):
>>> u = np.linspace(0, 2 * np.pi, 100) >>> v = np.linspace(0, np.pi, 100) >>> x = np.outer(np.cos(u), np.sin(v)) >>> y = np.outer(np.sin(u), np.sin(v)) >>> z = np.outer(np.ones(np.size(u)), np.cos(v)) >>> ax.plot_surface(x, y, z, color='y', alpha=0.1)對大量點進行插值可能會在球體表麵上提供平滑曲線的外觀,這對於球體表麵上的離散積分計算也很有用:
>>> start = np.array([1, 0, 0]) >>> end = np.array([0, 0, 1]) >>> t_vals = np.linspace(0, 1, 200) >>> result = geometric_slerp(start, ... end, ... t_vals) >>> ax.plot(result[...,0], ... result[...,1], ... result[...,2], ... c='k') >>> plt.show()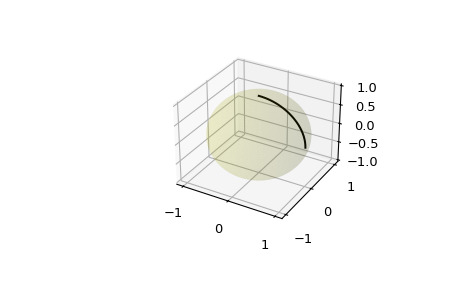
相關用法
- Python SciPy spatial.tsearch用法及代碼示例
- Python SciPy spatial.Voronoi用法及代碼示例
- Python SciPy spatial.procrustes用法及代碼示例
- Python SciPy spatial.SphericalVoronoi用法及代碼示例
- Python SciPy spatial.minkowski_distance用法及代碼示例
- Python SciPy spatial.HalfspaceIntersection用法及代碼示例
- Python SciPy spatial.voronoi_plot_2d用法及代碼示例
- Python SciPy spatial.minkowski_distance_p用法及代碼示例
- Python SciPy spatial.distance_matrix用法及代碼示例
- Python SciPy spatial.ConvexHull用法及代碼示例
- Python SciPy spatial.convex_hull_plot_2d用法及代碼示例
- Python SciPy spatial.Delaunay用法及代碼示例
- Python SciPy spatial.delaunay_plot_2d用法及代碼示例
- Python SciPy sparse.isspmatrix用法及代碼示例
- Python SciPy sparse.save_npz用法及代碼示例
- Python SciPy sparse.issparse用法及代碼示例
- Python SciPy sparse.coo_matrix用法及代碼示例
- Python SciPy sparse.isspmatrix_csc用法及代碼示例
- Python SciPy sparse.isspmatrix_csr用法及代碼示例
- Python SciPy sparse.tril用法及代碼示例
- Python SciPy sparse.coo_array用法及代碼示例
- Python SciPy sparse.dia_array用法及代碼示例
- Python SciPy sparse.bmat用法及代碼示例
- Python SciPy sparse.hstack用法及代碼示例
- Python SciPy sparse.rand用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.spatial.geometric_slerp。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
