Python SciPy spatial.HalfspaceIntersection用法及代碼示例

本文簡要介紹 python 語言中 scipy.spatial.HalfspaceIntersection 的用法。

用法:

class  scipy.spatial.HalfspaceIntersection(halfspaces, interior_point, incremental=False, qhull_options=None)#

N 維的半空間交點。

參數 ：：

halfspaces： 浮點數的ndarray，形狀(nineq，ndim+1)

Ax + b <= 0 形式的堆疊不等式，格式為 [A;乙]

interior_point： 浮點數的ndarray，形狀(ndim，)

清楚地指向由半空間定義的區域內。也稱為可行點，可以通過線性規劃得到。

incremental： 布爾型，可選

允許增量添加新的半空間。這會占用一些額外的資源。

qhull_options： str，可選

傳遞給 Qhull 的其他選項。有關詳細信息，請參閱 Qhull 手冊。 (默認值：“Qx” 用於 ndim > 4，否則為“”)選項 “H” 始終啟用。

拋出 ：：

QhullError

當 Qhull 遇到錯誤條件時引發，例如在未啟用解決選項時出現幾何退化。

ValueError

如果將不兼容的數組作為輸入給出，則引發。

注意：

使用 Qhull library 計算交點。這再現了 Qhull 的“qhalf” 函數。

參考：

[庫爾]

http://www.qhull.org/

[1]

S. Boyd、L. Vandenberghe，凸優化，可在 http://stanford.edu/~boyd/cvxbook/ 獲得

例子：

形成一些多邊形的平麵的半空間相交

>>> from scipy.spatial import HalfspaceIntersection
>>> import numpy as np
>>> halfspaces = np.array([[-1, 0., 0.],
...                        [0., -1., 0.],
...                        [2., 1., -4.],
...                        [-0.5, 1., -2.]])
>>> feasible_point = np.array([0.5, 0.5])
>>> hs = HalfspaceIntersection(halfspaces, feasible_point)

將半空間繪製為填充區域和交點：

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax = fig.add_subplot(1, 1, 1, aspect='equal')
>>> xlim, ylim = (-1, 3), (-1, 3)
>>> ax.set_xlim(xlim)
>>> ax.set_ylim(ylim)
>>> x = np.linspace(-1, 3, 100)
>>> symbols = ['-', '+', 'x', '*']
>>> signs = [0, 0, -1, -1]
>>> fmt = {"color": None, "edgecolor": "b", "alpha": 0.5}
>>> for h, sym, sign in zip(halfspaces, symbols, signs):
...     hlist = h.tolist()
...     fmt["hatch"] = sym
...     if h[1]== 0:
...         ax.axvline(-h[2]/h[0], label='{}x+{}y+{}=0'.format(*hlist))
...         xi = np.linspace(xlim[sign], -h[2]/h[0], 100)
...         ax.fill_between(xi, ylim[0], ylim[1], **fmt)
...     else:
...         ax.plot(x, (-h[2]-h[0]*x)/h[1], label='{}x+{}y+{}=0'.format(*hlist))
...         ax.fill_between(x, (-h[2]-h[0]*x)/h[1], ylim[sign], **fmt)
>>> x, y = zip(*hs.intersections)
>>> ax.plot(x, y, 'o', markersize=8)

默認情況下，qhull 不提供計算內點的方法。這可以很容易地使用線性規劃來計算。考慮 \(Ax + b \leq 0\) 形式的半空間，求解線性程序：

\[ \begin{align}\begin{aligned}max \: y\\s.t. Ax + y ||A_i|| \leq -b\end{aligned}\end{align} \]

\(A_i\) 是 A 的行，即每個平麵的法線。

將產生一個在凸多麵體內部最遠的點 x。準確地說，它是多麵體中半徑為 y 的最大超球麵的中心。該點稱為多麵體的切比雪夫中心(參見 [1] 4.3.1，pp148-149)。 Qhull 輸出的方程總是被歸一化的。

>>> from scipy.optimize import linprog
>>> from matplotlib.patches import Circle
>>> norm_vector = np.reshape(np.linalg.norm(halfspaces[:, :-1], axis=1),
...     (halfspaces.shape[0], 1))
>>> c = np.zeros((halfspaces.shape[1],))
>>> c[-1] = -1
>>> A = np.hstack((halfspaces[:, :-1], norm_vector))
>>> b = - halfspaces[:, -1:]
>>> res = linprog(c, A_ub=A, b_ub=b, bounds=(None, None))
>>> x = res.x[:-1]
>>> y = res.x[-1]
>>> circle = Circle(x, radius=y, alpha=0.3)
>>> ax.add_patch(circle)
>>> plt.legend(bbox_to_anchor=(1.6, 1.0))
>>> plt.show()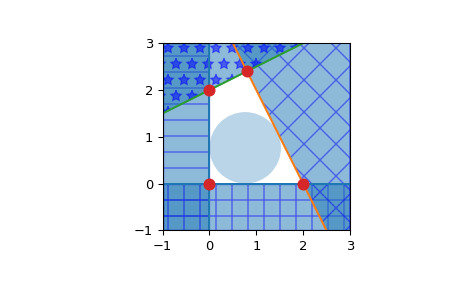

屬性 ：：

halfspaces： ndarray of double, shape (nineq, ndim+1)

輸入半空格。

interior_point :ndarray of floats, shape (ndim,)：

輸入內點。

intersections： ndarray of double, shape (ninter, ndim)

所有半空間的交點。

dual_points： ndarray of double, shape (nineq, ndim)

輸入半空間的對偶點。

dual_facets： 整數列表列表

形成雙凸包的(不一定是單純的)麵的點的索引。

dual_vertices： 整數的ndarray，形狀(nvertices，)

形成雙凸包頂點的半空間索引。對於二維凸包，頂點按逆時針順序排列。對於其他維度，它們按輸入順序排列。

dual_equations： ndarray of double, shape (nfacet, ndim+1)

[normal, offset] 形成雙麵的超平麵方程(更多信息請參見Qhull documentation)。

dual_area： 浮點數

雙凸包麵積

dual_volume： 浮點數

雙凸包的體積