Python SciPy spatial.SphericalVoronoi用法及代碼示例

本文簡要介紹 python 語言中 scipy.spatial.SphericalVoronoi 的用法。

用法:

class  scipy.spatial.SphericalVoronoi(points, radius=1, center=None, threshold=1e-06)#

Voronoi 球體表麵的圖表。

參數 ：：

points： 浮點數數組，形狀(npoints，ndim)

用於構造球形Voronoi 圖的點的坐標。

radius： 浮點數，可選

球體半徑(默認值：1)

center： 浮點數的ndarray，形狀(ndim，)

球心(默認：原點)

threshold： 浮點數

用於檢測點和球體參數之間的重複點和不匹配的閾值。 (默認值：1e-06)

拋出 ：：

ValueError

如果有重複的點。如果提供的半徑與點不一致。

注意：

球形Voronoi 圖算法的執行過程如下。計算輸入點(生成器)的凸包，相當於它們在球體表麵上的 Delaunay 三角剖分 [Caroli]。然後使用凸包鄰居信息對每個生成器周圍的 Voronoi 區域頂點進行排序。與 Voronoi 區域頂點排序的基於角度的方法相比，後一種方法對浮點問題的敏感度要低得多。

球形Voronoi算法性能的經驗評估表明二次時間複雜度(對數線性是最佳的，但算法實現起來更具挑戰性)。

參考：

[卡羅利]

卡羅利等人。對球體上或球體附近的點進行穩健且高效的 Delaunay 三角剖分。研究報告 RR-7004，2009。

[VanOosterom]

範 Oosterom 和 Strackee。平麵三角形的立體角。 IEEE Transactions on Biomedical Engineering, 2, 1983, pp 125-126。

例子：

做一些導入並在立方體上取一些點：

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.spatial import SphericalVoronoi, geometric_slerp
>>> from mpl_toolkits.mplot3d import proj3d
>>> # set input data
>>> points = np.array([[0, 0, 1], [0, 0, -1], [1, 0, 0],
...                    [0, 1, 0], [0, -1, 0], [-1, 0, 0], ])

計算球麵Voronoi圖：

>>> radius = 1
>>> center = np.array([0, 0, 0])
>>> sv = SphericalVoronoi(points, radius, center)

生成圖：

>>> # sort vertices (optional, helpful for plotting)
>>> sv.sort_vertices_of_regions()
>>> t_vals = np.linspace(0, 1, 2000)
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111, projection='3d')
>>> # plot the unit sphere for reference (optional)
>>> u = np.linspace(0, 2 * np.pi, 100)
>>> v = np.linspace(0, np.pi, 100)
>>> x = np.outer(np.cos(u), np.sin(v))
>>> y = np.outer(np.sin(u), np.sin(v))
>>> z = np.outer(np.ones(np.size(u)), np.cos(v))
>>> ax.plot_surface(x, y, z, color='y', alpha=0.1)
>>> # plot generator points
>>> ax.scatter(points[:, 0], points[:, 1], points[:, 2], c='b')
>>> # plot Voronoi vertices
>>> ax.scatter(sv.vertices[:, 0], sv.vertices[:, 1], sv.vertices[:, 2],
...                    c='g')
>>> # indicate Voronoi regions (as Euclidean polygons)
>>> for region in sv.regions:
...    n = len(region)
...    for i in range(n):
...        start = sv.vertices[region][i]
...        end = sv.vertices[region][(i + 1) % n]
...        result = geometric_slerp(start, end, t_vals)
...        ax.plot(result[..., 0],
...                result[..., 1],
...                result[..., 2],
...                c='k')
>>> ax.azim = 10
>>> ax.elev = 40
>>> _ = ax.set_xticks([])
>>> _ = ax.set_yticks([])
>>> _ = ax.set_zticks([])
>>> fig.set_size_inches(4, 4)
>>> plt.show()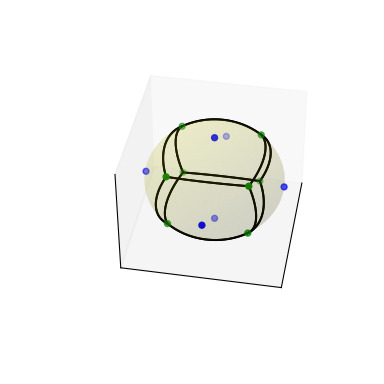

屬性 ：：

points： 形狀的雙數組(npoints，ndim)

ndim 維度中的點以從中生成Voronoi 圖

radius： 雙倍的

球體半徑

center： 形狀的雙數組 (ndim,)

球心

vertices： 形狀的雙數組(nvertices，ndim)

Voronoi頂點對應點

regions： 形狀整數列表列表 (npoints, _ )

n-th 條目是一個列表，由屬於 n-th 點的頂點的索引組成，以點為單位