Python SciPy optimize.least_squares用法及代码示例

本文简要介绍 python 语言中 scipy.optimize.least_squares 的用法。

用法:

scipy.optimize.least_squares(fun, x0, jac='2-point', bounds=(-inf, inf), method='trf', ftol=1e-08, xtol=1e-08, gtol=1e-08, x_scale=1.0, loss='linear', f_scale=1.0, diff_step=None, tr_solver=None, tr_options={}, jac_sparsity=None, max_nfev=None, verbose=0, args=(), kwargs={})#

求解具有变量界限的非线性最小二乘问题。

给定残差 f(x)(n 个实变量的 m-D 实函数)和损失函数 rho(s)(标量函数)，least_squares 找到成本函数 F(x) 的局部最小值：

minimize F(x) = 0.5 * sum(rho(f_i(x)**2), i = 0, ..., m - 1)
subject to lb <= x <= ub

损失函数 rho(s) 的目的是减少异常值对解的影响。

参数 ：：

fun： 可调用的

计算残差向量的函数，签名为 fun(x, *args, **kwargs) ，即最小化相对于其第一个参数进行。传递给此函数的参数x 是一个形状为 (n,) 的 ndarray(绝不是标量，即使 n=1 也是如此)。它必须分配并返回一个形状为 (m,) 或标量的一维数组。如果参数 x 是复数或函数 fun 返回复数残差，则必须将其包装在实参数的实函数中，如示例部分末尾所示。

x0： 数组 形状为 (n,) 或浮点数

对自变量的初步猜测。如果是浮点数，它将被视为具有一个元素的一维数组。

jac： {‘2-point’, ‘3-point’, ‘cs’, callable}, 可选

计算雅可比矩阵的方法(m-by-n 矩阵，其中元素 (i, j) 是 f[i] 对 x[j] 的偏导数)。关键字选择用于数值估计的有限差分方案。方案“3-point”更准确，但需要的操作数是“2-point”(默认)的两倍。方案‘cs’ 使用复杂的步骤，虽然可能是最准确的，但它仅适用于乐趣正确处理复杂的输入，并且可以分析地继续到复杂的平面。方法 ‘lm’ 始终使用“2 点”方案。如果可调用，则用作jac(x, *args, **kwargs)并且应该返回雅可比行列式的良好近似值(或精确值)作为 数组(应用 np.atleast_2d)、稀疏矩阵(csr_matrix 首选性能)或scipy.sparse.linalg.LinearOperator.

bounds： 数组 或 Bounds 的 2 元组，可选

指定边界有两种方法：

1. Instance of Bounds class

2. Lower and upper bounds on independent variables. Defaults to no bounds. Each array must match the size of x0 or be a scalar, in the latter case a bound will be the same for all variables. Use np.inf with an appropriate sign to disable bounds on all or some variables.

method： {‘trf’, ‘dogbox’, ‘lm’}，可选

执行最小化的算法。

• ‘trf’ : Trust Region Reflective algorithm, particularly suitable for large sparse problems with bounds. Generally robust method.

• ‘dogbox’ : dogleg algorithm with rectangular trust regions, typical use case is small problems with bounds. Not recommended for problems with rank-deficient Jacobian.

• ‘lm’ : Levenberg-Marquardt algorithm as implemented in MINPACK. Doesn’t handle bounds and sparse Jacobians. Usually the most efficient method for small unconstrained problems.

默认为‘trf’。有关详细信息，请参阅注释。

ftol： 浮点数或无，可选

因成本函数变化而终止的容差。默认值为 1e-8。当 dF < ftol * F 时停止优化过程，并且在最后一步中局部二次模型与真实模型之间存在足够的一致性。

如果 None 并且 ‘method’ 不是 ‘lm’，则禁用此条件的终止。如果‘method’ 是‘lm’，则此容差必须高于机器 epsilon。

xtol： 浮点数或无，可选

因自变量变化而终止的容差。默认值为 1e-8。确切的条件取决于使用的方法：

• For ‘trf’ and ‘dogbox’ : norm(dx) < xtol * (xtol + norm(x)).

• For ‘lm’ : Delta < xtol * norm(xs), where Delta is a trust-region radius and xs is the value of x scaled according to x_scale parameter (see below).

如果 None 并且 ‘method’ 不是 ‘lm’，则禁用此条件的终止。如果‘method’ 是‘lm’，则此容差必须高于机器 epsilon。

gtol： 浮点数或无，可选

梯度范数终止的容差。默认值为 1e-8。确切的条件取决于使用的方法：

• For ‘trf’ : norm(g_scaled, ord=np.inf) < gtol, where g_scaled is the value of the gradient scaled to account for the presence of the bounds [STIR].

• For ‘dogbox’ : norm(g_free, ord=np.inf) < gtol, where g_free is the gradient with respect to the variables which are not in the optimal state on the boundary.

• For ‘lm’ : the maximum absolute value of the cosine of angles between columns of the Jacobian and the residual vector is less than gtol, or the residual vector is zero.

如果 None 并且 ‘method’ 不是 ‘lm’，则禁用此条件的终止。如果‘method’ 是‘lm’，则此容差必须高于机器 epsilon。

x_scale： 数组 或‘jac’，可选

每个变量的特征尺度。环境x_scale相当于用缩放变量重新表述问题xs = x / x_scale.另一种观点是，信任区域沿第 j 维的大小与x_scale[j].可以通过设置来提高收敛性x_scale这样沿着任何缩放变量的给定大小的步长对成本函数都有类似的影响。如果设置为‘jac’，则使用雅可比矩阵列的逆范数迭代更新比例(如在[JJ更多])。

loss： str 或可调用，可选

确定损失函数。允许使用以下关键字值：

• ‘linear’ (default) : rho(z) = z. Gives a standard least-squares problem.

• ‘soft_l1’ : rho(z) = 2 * ((1 + z)**0.5 - 1). The smooth approximation of l1 (absolute value) loss. Usually a good choice for robust least squares.

• ‘huber’ : rho(z) = z if z <= 1 else 2*z**0.5 - 1. Works similarly to ‘soft_l1’.

• ‘cauchy’ : rho(z) = ln(1 + z). Severely weakens outliers influence, but may cause difficulties in optimization process.

• ‘arctan’ : rho(z) = arctan(z). Limits a maximum loss on a single residual, has properties similar to ‘cauchy’.

如果可调用，它必须采用一维 ndarray z=f**2 并返回形状为 (3, m) 的 数组，其中第 0 行包含函数值，第 1 行包含一阶导数，第 2 行包含二阶导数。方法 ‘lm’ 仅支持 ‘linear’ 损失。

f_scale： 浮点数，可选

内部和异常残差之间的软边距值，默认为 1.0。损失函数评估如下rho_(f**2) = C**2 * rho(f**2 / C**2)，其中C是f_scale， 和rho由失利范围。该参数与loss='linear', 但对于其他失利值是至关重要的。

max_nfev： 无或整数，可选

终止前函数评估的最大次数。如果 None (默认)，则自动选择该值：

• For ‘trf’ and ‘dogbox’ : 100 * n.

• For ‘lm’ : 100 * n if jac is callable and 100 * n * (n + 1) otherwise (because ‘lm’ counts function calls in Jacobian estimation).

diff_step： 无或类似数组，可选

确定雅可比行列式的有限差分逼近的相对步长。实际步长计算为x * diff_step.如果无(默认)，则diff_step被视为使用的有限差分方案的机器 epsilon 的常规 “optimal” 幂[NR].

tr_solver： {无，‘exact’, ‘lsmr’}，可选

解决trust-region子问题的方法，仅与‘trf’和‘dogbox’方法相关。

• ‘exact’ is suitable for not very large problems with dense Jacobian matrices. The computational complexity per iteration is comparable to a singular value decomposition of the Jacobian matrix.

• ‘lsmr’ is suitable for problems with sparse and large Jacobian matrices. It uses the iterative procedure scipy.sparse.linalg.lsmr for finding a solution of a linear least-squares problem and only requires matrix-vector product evaluations.

如果 None (默认)，则根据第一次迭代返回的 Jacobian 类型选择求解器。

tr_options： 字典，可选

传递给 trust-region 求解器的关键字选项。

• tr_solver='exact': tr_options are ignored.

• tr_solver='lsmr': options for scipy.sparse.linalg.lsmr. Additionally, method='trf' supports ‘regularize’ option (bool, default is True), which adds a regularization term to the normal equation, which improves convergence if the Jacobian is rank-deficient [Byrd] (eq. 3.4).

jac_sparsity： {无，数组，稀疏矩阵}，可选

定义用于有限差分估计的雅可比矩阵的稀疏结构，其形状必须为 (m, n)。如果雅可比矩阵中只有少数非零元素每个行，提供稀疏结构将大大加快计算速度[柯蒂斯].零条目意味着雅可比行列式中的相应元素相同为零。如果提供，则强制使用 ‘lsmr’ trust-region 求解器。如果无(默认)，则将使用密集差分。对‘lm’ 方法无效。

verbose： {0, 1, 2}，可选

算法的详细程度：

• 0 (default) : work silently.

• 1 : display a termination report.

• 2 : display progress during iterations (not supported by ‘lm’ method).

args, kwargs： 元组和字典，可选

传递给的附加参数乐趣和江淮.默认情况下两者都是空的。调用签名是fun(x, *args, **kwargs)和同样的江淮.

返回 ：：

result： OptimizeResult

OptimizeResult 定义了以下字段：

x ndarray, shape (n,)

Solution found.

cost float

Value of the cost function at the solution.

fun ndarray, shape (m,)

Vector of residuals at the solution.

jac ndarray, sparse matrix or LinearOperator, shape (m, n)

Modified Jacobian matrix at the solution, in the sense that J^T J is a Gauss-Newton approximation of the Hessian of the cost function. The type is the same as the one used by the algorithm.

grad ndarray, shape (m,)

Gradient of the cost function at the solution.

optimality float

First-order optimality measure. In unconstrained problems, it is always the uniform norm of the gradient. In constrained problems, it is the quantity which was compared with gtol during iterations.

active_mask ndarray of int, shape (n,)

Each component shows whether a corresponding constraint is active (that is, whether a variable is at the bound):

• 0 : a constraint is not active.

• -1 : a lower bound is active.

• 1 : an upper bound is active.

Might be somewhat arbitrary for ‘trf’ method as it generates a sequence of strictly feasible iterates and active_mask is determined within a tolerance threshold.

nfev int

Number of function evaluations done. Methods ‘trf’ and ‘dogbox’ do not count function calls for numerical Jacobian approximation, as opposed to ‘lm’ method.

njev int or None

Number of Jacobian evaluations done. If numerical Jacobian approximation is used in ‘lm’ method, it is set to None.

status int

The reason for algorithm termination:

• -1 : improper input parameters status returned from MINPACK.

• 0 : the maximum number of function evaluations is exceeded.

• 1 : gtol termination condition is satisfied.

• 2 : ftol termination condition is satisfied.

• 3 : xtol termination condition is satisfied.

• 4 : Both ftol and xtol termination conditions are satisfied.

message str

Verbal description of the termination reason.

success bool

True if one of the convergence criteria is satisfied (status > 0).

注意：

方法 ‘lm’ (Levenberg-Marquardt) 调用 MINPACK(lmder、lmdif)中实现的最小二乘算法的包装器。它运行制定为 trust-region 类型算法的 Levenberg-Marquardt 算法。该实现基于论文[JJMore]，它非常健壮和高效，并且有很多聪明的技巧。对于无约束问题，它应该是您的首选。请注意，它不支持边界。而且，当 m < n 时它不起作用。

方法‘trf’(信任区域反射)的动机是求解方程组的过程，该方程组构成了[STIR]中阐述的bound-constrained最小化问题的first-order最优条件。该算法迭代地解决由特殊对角二次项增强的 trust-region 子问题，并具有由距边界的距离和梯度方向确定的 trust-region 形状。此增强函数有助于避免直接进入边界并有效地探索整个变量空间。为了进一步提高收敛性，该算法考虑了边界反映的搜索方向。为了满足理论要求，算法保持迭代严格可行。对于稠密雅可比行列式trust-region，子问题可以通过一种与 [JJMore] 中说明的方法非常相似的精确方法来解决(并在 MINPACK 中实现)。与 MINPACK 实现的不同之处在于每次迭代都会进行雅可比矩阵的奇异值分解，而不是 QR 分解和一系列吉文斯旋转消除。对于大型稀疏雅可比行列式，使用解决 trust-region 子问题的二维子空间方法 [STIR]、[Byrd]。该子空间由缩放梯度和 scipy.sparse.linalg.lsmr 提供的近似 Gauss-Newton 解决方案组成。当不施加任何约束时，该算法与 MINPACK 非常相似，并且通常具有可比的性能。该算法在无界和有界问题中都非常稳健，因此被选为默认算法。

方法‘dogbox’在trust-region框架中运行，但考虑矩形信任区域而不是传统的椭球体[Voglis]。当前信任区域和初始边界的交集再次是矩形，因此在每次迭代中，受边界约束的二次最小化问题可以通过鲍威尔狗腿法[NumOpt]近似解决。对于密集雅可比行列式，所需的 Gauss-Newton 步骤可以精确计算，对于大型稀疏雅可比行列式，可以通过 scipy.sparse.linalg.lsmr 近似计算。当雅可比行列式的秩小于变量的数量时，该算法可能会表现出缓慢的收敛性。在具有少量变量的有界问题中，该算法通常优于‘trf’。

鲁棒损失函数的实现如[BA]中所述。这个想法是在每次迭代时修改残差向量和雅可比矩阵，使得计算的梯度和Gauss-Newton Hessian 近似与成本函数的真实梯度和 Hessian 近似相匹配。然后算法以正常方式进行，即鲁棒损失函数被实现为标准最小二乘算法的简单包装。

参考：

[STIR] (1,2,3)

M. A. Branch、T. F. Coleman 和 Y. Li，“Large-Scale Bound-Constrained 最小化问题的子空间、内部和共轭梯度方法”，SIAM 科学计算杂志，卷。 21，第 1 期，第 1-23 页，1999 年。

[NR]

威廉 H. 出版社等。 al.，“数字食谱。科学计算的艺术。第三版”，秒。 5.7.

[伯德] (1,2)

R. H. Byrd、R. B. Schnabel 和 G. A. Shultz，“通过在二维子空间上最小化的信任域问题的近似解”，数学。编程，40，第 247-263 页，1988 年。

[柯蒂斯]

A. Curtis、M. J. D. Powell 和 J. Reid，“关于稀疏雅可比矩阵的估计”，数学研究所及其应用杂志，13，第 117-120 页，1974 年。

[JJ更多] (1,2,3)

J. J. More，“Levenberg-Marquardt 算法：实现和理论”，数值分析，编辑。 G. A. Watson，数学讲义 630，Springer Verlag，第 105-116 页，1977 年。

[沃格利斯]

C. Voglis 和 I. E. Lagaris，“A Rectangular Trust Region Dogleg Approach for Unconstrained and Bound Constrained Nonlinear Optimization”，WSEAS 国际应用数学会议，希腊科孚岛，2004 年。

[NumOpt]

J. Nocedal 和 S. J. Wright，“数值优化，第 2 版”，第 4 章。

[BA]

B.特里格斯等。 al.，“Bundle Adjustment - A Modern Synthesis”，视觉算法国际研讨会论文集：理论与实践，第 298-372 页，1999 年。

例子：

在这个例子中，我们找到了一个对自变量没有限制的 Rosenbrock 函数的最小值。

>>> import numpy as np
>>> def fun_rosenbrock(x):
...     return np.array([10 * (x[1] - x[0]**2), (1 - x[0])])

请注意，我们只提供残差的向量。该算法将成本函数构造为残差的平方和，从而给出 Rosenbrock 函数。确切的最小值在 x = [1.0, 1.0] 。

>>> from scipy.optimize import least_squares
>>> x0_rosenbrock = np.array([2, 2])
>>> res_1 = least_squares(fun_rosenbrock, x0_rosenbrock)
>>> res_1.x
array([ 1.,  1.])
>>> res_1.cost
9.8669242910846867e-30
>>> res_1.optimality
8.8928864934219529e-14

我们现在约束变量，使之前的解决方案变得不可行。具体来说，我们要求x[1] >= 1.5， 和x[0]不受约束。为此，我们指定界限参数为least_squares在表格中bounds=([-np.inf, 1.5], np.inf).

我们还提供解析雅可比行列式：

>>> def jac_rosenbrock(x):
...     return np.array([
...         [-20 * x[0], 10],
...         [-1, 0]])

把这一切放在一起，我们看到新的解决方案是有限的：

>>> res_2 = least_squares(fun_rosenbrock, x0_rosenbrock, jac_rosenbrock,
...                       bounds=([-np.inf, 1.5], np.inf))
>>> res_2.x
array([ 1.22437075,  1.5       ])
>>> res_2.cost
0.025213093946805685
>>> res_2.optimality
1.5885401433157753e-07

现在我们求解一个包含 100000 个变量的 Broyden 三对角函数 vector-valued 的方程组(即，成本函数至少应为零)：

>>> def fun_broyden(x):
...     f = (3 - x) * x + 1
...     f[1:] -= x[:-1]
...     f[:-1] -= 2 * x[1:]
...     return f

对应的雅可比矩阵是稀疏的。我们告诉算法通过有限差分来估计它，并提供雅可比的稀疏结构来显著加速这个过程。

>>> from scipy.sparse import lil_matrix
>>> def sparsity_broyden(n):
...     sparsity = lil_matrix((n, n), dtype=int)
...     i = np.arange(n)
...     sparsity[i, i] = 1
...     i = np.arange(1, n)
...     sparsity[i, i - 1] = 1
...     i = np.arange(n - 1)
...     sparsity[i, i + 1] = 1
...     return sparsity
...
>>> n = 100000
>>> x0_broyden = -np.ones(n)
...
>>> res_3 = least_squares(fun_broyden, x0_broyden,
...                       jac_sparsity=sparsity_broyden(n))
>>> res_3.cost
4.5687069299604613e-23
>>> res_3.optimality
1.1650454296851518e-11

让我们还使用稳健的损失函数来解决曲线拟合问题，以处理数据中的异常值。将模型函数定义为 y = a + b * exp(c * t) ，其中 t 是预测变量，y 是观察值，a、b、c 是要估计的参数。

首先，定义生成带有噪声和异常值的数据的函数，定义模型参数并生成数据：

>>> from numpy.random import default_rng
>>> rng = default_rng()
>>> def gen_data(t, a, b, c, noise=0., n_outliers=0, seed=None):
...     rng = default_rng(seed)
...
...     y = a + b * np.exp(t * c)
...
...     error = noise * rng.standard_normal(t.size)
...     outliers = rng.integers(0, t.size, n_outliers)
...     error[outliers] *= 10
...
...     return y + error
...
>>> a = 0.5
>>> b = 2.0
>>> c = -1
>>> t_min = 0
>>> t_max = 10
>>> n_points = 15
...
>>> t_train = np.linspace(t_min, t_max, n_points)
>>> y_train = gen_data(t_train, a, b, c, noise=0.1, n_outliers=3)

定义用于计算残差和参数初始估计的函数。

>>> def fun(x, t, y):
...     return x[0] + x[1] * np.exp(x[2] * t) - y
...
>>> x0 = np.array([1.0, 1.0, 0.0])

计算标准最小二乘解：

>>> res_lsq = least_squares(fun, x0, args=(t_train, y_train))

现在计算两个具有两个不同鲁棒损失函数的解决方案。参数 f_scale 设置为 0.1，这意味着内部残差不应显著超过 0.1(使用的噪声水平)。

>>> res_soft_l1 = least_squares(fun, x0, loss='soft_l1', f_scale=0.1,
...                             args=(t_train, y_train))
>>> res_log = least_squares(fun, x0, loss='cauchy', f_scale=0.1,
...                         args=(t_train, y_train))

最后，绘制所有曲线。我们看到，通过选择适当的损失，即使存在强异常值，我们也可以获得接近最优的估计值。但请记住，通常建议先尝试‘soft_l1’ 或‘huber’ 损失(如果有必要)，因为其他两个选项可能会导致优化过程中的困难。

>>> t_test = np.linspace(t_min, t_max, n_points * 10)
>>> y_true = gen_data(t_test, a, b, c)
>>> y_lsq = gen_data(t_test, *res_lsq.x)
>>> y_soft_l1 = gen_data(t_test, *res_soft_l1.x)
>>> y_log = gen_data(t_test, *res_log.x)
...
>>> import matplotlib.pyplot as plt
>>> plt.plot(t_train, y_train, 'o')
>>> plt.plot(t_test, y_true, 'k', linewidth=2, label='true')
>>> plt.plot(t_test, y_lsq, label='linear loss')
>>> plt.plot(t_test, y_soft_l1, label='soft_l1 loss')
>>> plt.plot(t_test, y_log, label='cauchy loss')
>>> plt.xlabel("t")
>>> plt.ylabel("y")
>>> plt.legend()
>>> plt.show()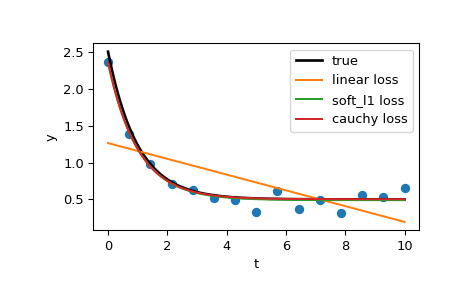

在下一个示例中，我们将展示如何使用 least_squares() 优化复变量的 complex-valued 残差函数。考虑以下函数：

>>> def f(z):
...     return z - (0.5 + 0.5j)

我们将其包装成一个实变量函数，该函数通过简单地将实部和虚部作为自变量处理来返回实数残差：

>>> def f_wrap(x):
...     fx = f(x[0] + 1j*x[1])
...     return np.array([fx.real, fx.imag])

因此，我们优化 2n 个实变量的 2m-D 实函数，而不是原来的 m-D n 个复变量的复函数：

>>> from scipy.optimize import least_squares
>>> res_wrapped = least_squares(f_wrap, (0.1, 0.1), bounds=([0, 0], [1, 1]))
>>> z = res_wrapped.x[0] + res_wrapped.x[1]*1j
>>> z
(0.49999999999925893+0.49999999999925893j)