Augment 接受模型对象和数据集，并添加有关数据集中每个观察值的信息。最常见的是，这包括 .fitted 列中的预测值、.resid 列中的残差以及 .se.fit 列中拟合值的标准误差。新列始终以 . 前缀开头，以避免覆盖原始数据集中的列。
用户可以通过 data 参数或 newdata 参数传递数据以进行增强。如果用户将数据传递给 data 参数，则它必须正是用于拟合模型对象的数据。将数据集传递给 newdata 以扩充模型拟合期间未使用的数据。这仍然要求至少存在用于拟合模型的所有预测变量列。如果用于拟合模型的原始结果变量未包含在 newdata 中，则输出中不会包含 .resid 列。
根据是否给出 data 或 newdata，增强的行为通常会有所不同。这是因为通常存在与训练观察(例如影响或相关)测量相关的信息，而这些信息对于新观察没有有意义的定义。
为了方便起见，许多增强方法提供默认的 data 参数，以便 augment(fit) 将返回增强的训练数据。在这些情况下，augment 尝试根据模型对象重建原始数据，并取得了不同程度的成功。
增强数据集始终以 tibble::tibble 形式返回，其行数与传递的数据集相同。这意味着传递的数据必须可强制转换为 tibble。如果预测变量将模型作为协变量矩阵的一部分输入，例如当模型公式使用 splines::ns() 、 stats::poly() 或 survival::Surv() 时，它会表示为矩阵列。
我们正在定义适合各种 na.action 参数的模型的行为，但目前不保证数据丢失时的行为。
参数
- x
-
从
poLCA::poLCA()返回的poLCA对象。 - data
-
base::data.frame 或
tibble::tibble()包含用于生成对象x的原始数据。默认为stats::model.frame(x)，以便augment(my_fit)返回增强的原始数据。不要将新数据传递给data参数。增强将报告传递给data参数的数据的影响和烹饪距离等信息。这些度量仅针对原始训练数据定义。 - ...
-
附加参数。不曾用过。仅需要匹配通用签名。注意：拼写错误的参数将被吸收到
...中，并被忽略。如果拼写错误的参数有默认值，则将使用默认值。例如，如果您传递conf.lvel = 0.9，所有计算将使用conf.level = 0.95进行。这里有两个异常：
细节
如果给出 data 参数，则这些列将包含在输出中(仅可以进行预测的行)。否则，将使用 poLCA 对象的 y 元素(其中包含用于拟合模型的清单变量)以及 x 中的任何协变量(如果存在)。
请注意，虽然所有类(不仅仅是预测模态类)的概率都可以在 posterior 元素中找到，但这些不包含在增强输出中。
也可以看看
其他 poLCA 整理器：glance.poLCA() 、tidy.poLCA()
例子
# load libraries for models and data
library(poLCA)
#> Loading required package: scatterplot3d
library(dplyr)
# generate data
data(values)
f <- cbind(A, B, C, D) ~ 1
# fit model
M1 <- poLCA(f, values, nclass = 2, verbose = FALSE)
M1
#> Conditional item response (column) probabilities,
#> by outcome variable, for each class (row)
#>
#> $A
#> Pr(1) Pr(2)
#> class 1: 0.2864 0.7136
#> class 2: 0.0068 0.9932
#>
#> $B
#> Pr(1) Pr(2)
#> class 1: 0.6704 0.3296
#> class 2: 0.0602 0.9398
#>
#> $C
#> Pr(1) Pr(2)
#> class 1: 0.6460 0.3540
#> class 2: 0.0735 0.9265
#>
#> $D
#> Pr(1) Pr(2)
#> class 1: 0.8676 0.1324
#> class 2: 0.2309 0.7691
#>
#> Estimated class population shares
#> 0.7208 0.2792
#>
#> Predicted class memberships (by modal posterior prob.)
#> 0.6713 0.3287
#>
#> =========================================================
#> Fit for 2 latent classes:
#> =========================================================
#> number of observations: 216
#> number of estimated parameters: 9
#> residual degrees of freedom: 6
#> maximum log-likelihood: -504.4677
#>
#> AIC(2): 1026.935
#> BIC(2): 1057.313
#> G^2(2): 2.719922 (Likelihood ratio/deviance statistic)
#> X^2(2): 2.719764 (Chi-square goodness of fit)
#>
# summarize model fit with tidiers + visualization
tidy(M1)
#> # A tibble: 16 × 5
#> variable class outcome estimate std.error
#> <chr> <int> <dbl> <dbl> <dbl>
#> 1 A 1 1 0.286 0.0393
#> 2 A 2 1 0.00681 0.0254
#> 3 A 1 2 0.714 0.0393
#> 4 A 2 2 0.993 0.0254
#> 5 B 1 1 0.670 0.0489
#> 6 B 2 1 0.0602 0.0649
#> 7 B 1 2 0.330 0.0489
#> 8 B 2 2 0.940 0.0649
#> 9 C 1 1 0.646 0.0482
#> 10 C 2 1 0.0735 0.0642
#> 11 C 1 2 0.354 0.0482
#> 12 C 2 2 0.927 0.0642
#> 13 D 1 1 0.868 0.0379
#> 14 D 2 1 0.231 0.0929
#> 15 D 1 2 0.132 0.0379
#> 16 D 2 2 0.769 0.0929
augment(M1)
#> # A tibble: 216 × 7
#> A B C D X.Intercept. .class .probability
#> <dbl> <dbl> <dbl> <dbl> <dbl> <int> <dbl>
#> 1 2 2 2 2 1 2 0.959
#> 2 2 2 2 2 1 2 0.959
#> 3 2 2 2 2 1 2 0.959
#> 4 2 2 2 2 1 2 0.959
#> 5 2 2 2 2 1 2 0.959
#> 6 2 2 2 2 1 2 0.959
#> 7 2 2 2 2 1 2 0.959
#> 8 2 2 2 2 1 2 0.959
#> 9 2 2 2 2 1 2 0.959
#> 10 2 2 2 2 1 2 0.959
#> # ℹ 206 more rows
glance(M1)
#> # A tibble: 1 × 8
#> logLik AIC BIC g.squared chi.squared df df.residual nobs
#> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <int>
#> 1 -504. 1027. 1057. 2.72 2.72 9 6 216
library(ggplot2)
ggplot(tidy(M1), aes(factor(class), estimate, fill = factor(outcome))) +
geom_bar(stat = "identity", width = 1) +
facet_wrap(~variable)
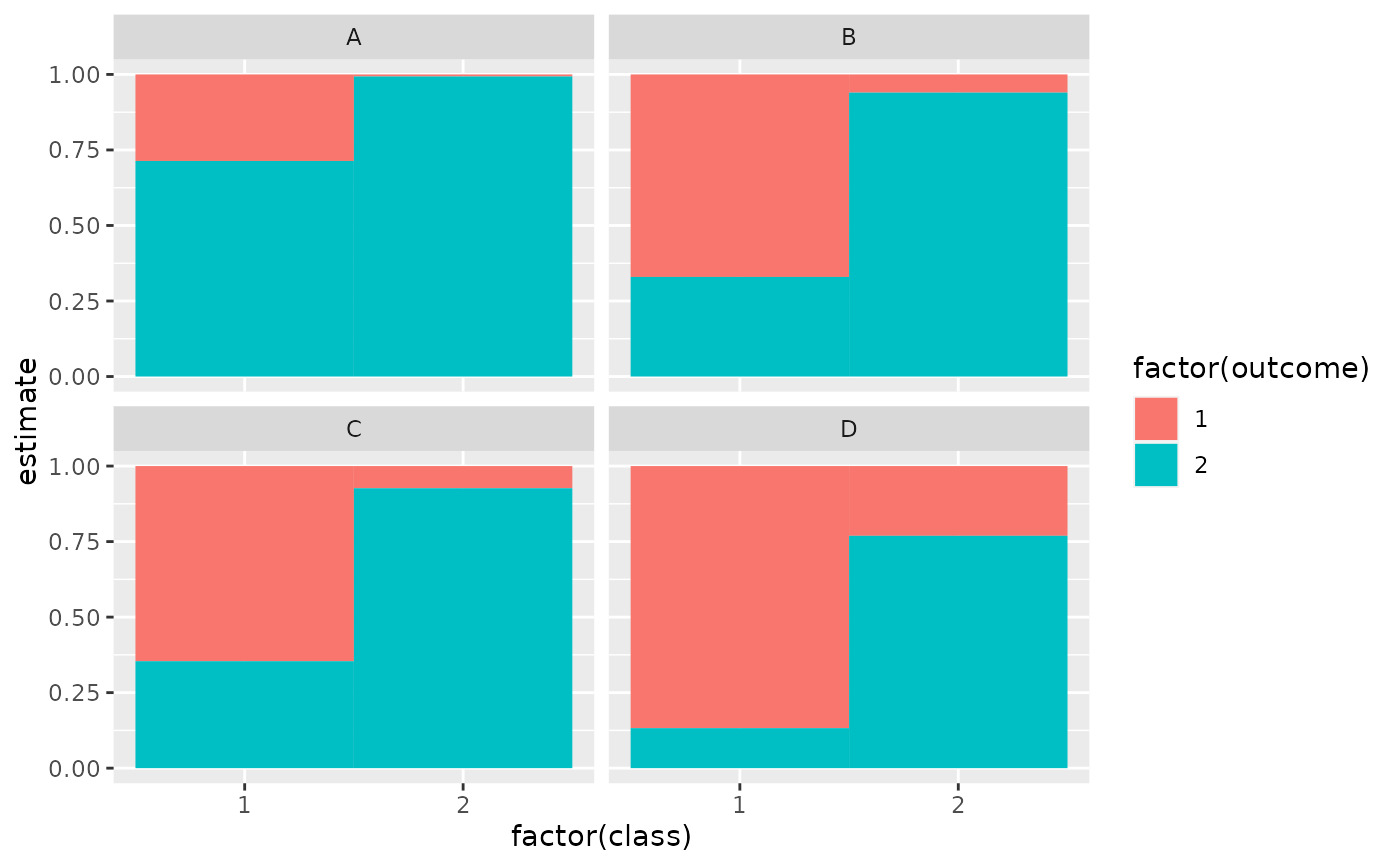# three-class model with a single covariate.
data(election)
f2a <- cbind(
MORALG, CARESG, KNOWG, LEADG, DISHONG, INTELG,
MORALB, CARESB, KNOWB, LEADB, DISHONB, INTELB
) ~ PARTY
nes2a <- poLCA(f2a, election, nclass = 3, nrep = 5, verbose = FALSE)
td <- tidy(nes2a)
td
#> # A tibble: 144 × 5
#> variable class outcome estimate std.error
#> <chr> <int> <fct> <dbl> <dbl>
#> 1 MORALG 1 1 Extremely well 0.108 0.0175
#> 2 MORALG 2 1 Extremely well 0.137 0.0182
#> 3 MORALG 3 1 Extremely well 0.622 0.0309
#> 4 MORALG 1 2 Quite well 0.383 0.0274
#> 5 MORALG 2 2 Quite well 0.668 0.0247
#> 6 MORALG 3 2 Quite well 0.335 0.0293
#> 7 MORALG 1 3 Not too well 0.304 0.0253
#> 8 MORALG 2 3 Not too well 0.180 0.0208
#> 9 MORALG 3 3 Not too well 0.0172 0.00841
#> 10 MORALG 1 4 Not well at all 0.205 0.0243
#> # ℹ 134 more rows
ggplot(td, aes(outcome, estimate, color = factor(class), group = class)) +
geom_line() +
facet_wrap(~variable, nrow = 2) +
theme(axis.text.x = element_text(angle = 90, hjust = 1))
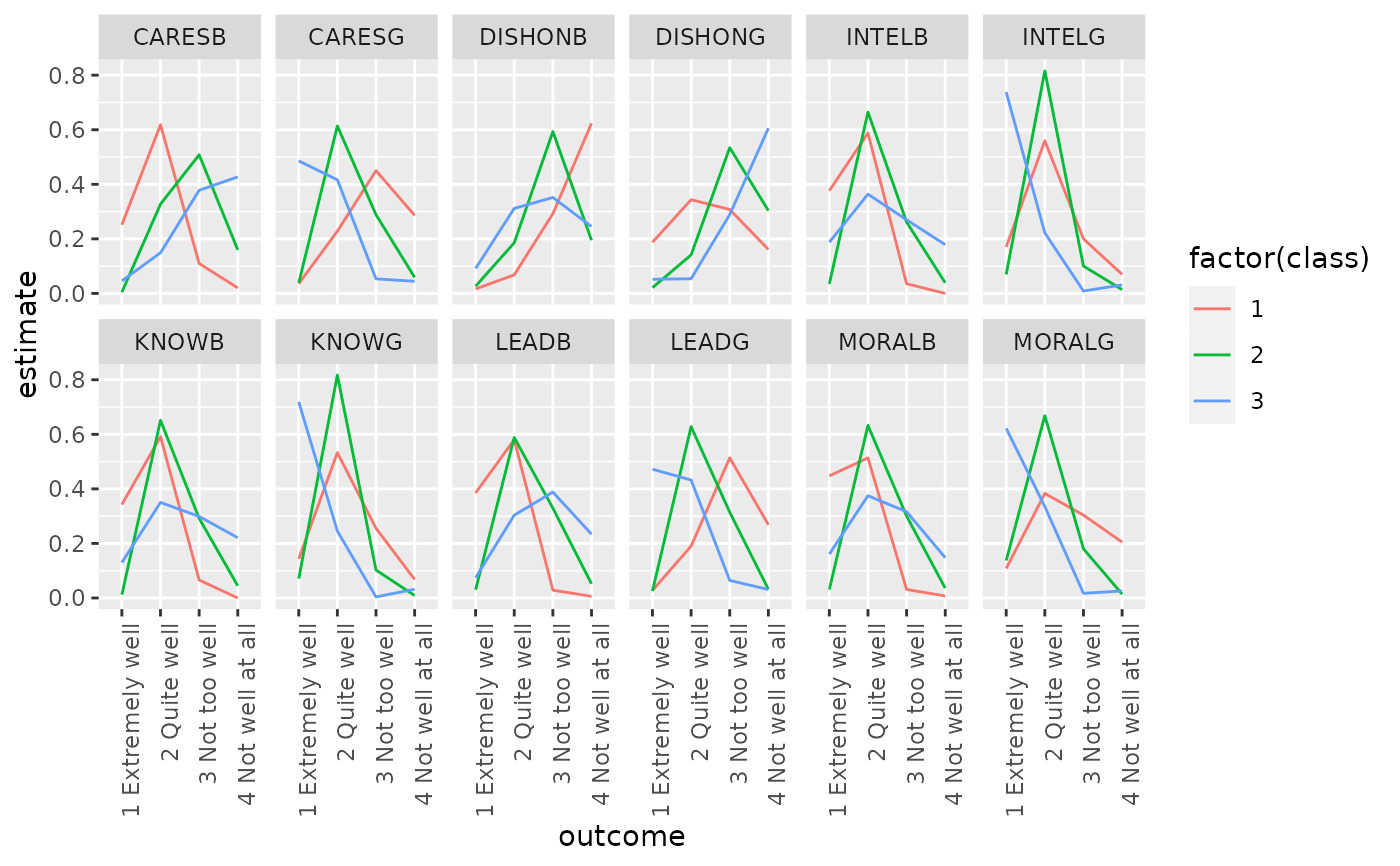au <- augment(nes2a)
au
#> # A tibble: 1,300 × 16
#> MORALG CARESG KNOWG LEADG DISHONG INTELG MORALB CARESB KNOWB LEADB
#> <fct> <fct> <fct> <fct> <fct> <fct> <fct> <fct> <fct> <fct>
#> 1 3 Not too … 1 Ext… 2 Qu… 2 Qu… 3 Not … 2 Qui… 1 Ext… 1 Ext… 2 Qu… 2 Qu…
#> 2 1 Extremel… 2 Qui… 2 Qu… 1 Ex… 3 Not … 2 Qui… 2 Qui… 2 Qui… 2 Qu… 3 No…
#> 3 2 Quite we… 2 Qui… 2 Qu… 2 Qu… 2 Quit… 2 Qui… 2 Qui… 3 Not… 2 Qu… 2 Qu…
#> 4 2 Quite we… 4 Not… 2 Qu… 3 No… 2 Quit… 2 Qui… 1 Ext… 1 Ext… 2 Qu… 2 Qu…
#> 5 2 Quite we… 2 Qui… 2 Qu… 2 Qu… 3 Not … 2 Qui… 3 Not… 4 Not… 4 No… 4 No…
#> 6 2 Quite we… 2 Qui… 2 Qu… 3 No… 4 Not … 2 Qui… 2 Qui… 3 Not… 2 Qu… 2 Qu…
#> 7 1 Extremel… 1 Ext… 1 Ex… 1 Ex… 4 Not … 1 Ext… 2 Qui… 4 Not… 2 Qu… 3 No…
#> 8 2 Quite we… 2 Qui… 2 Qu… 2 Qu… 3 Not … 2 Qui… 3 Not… 2 Qui… 2 Qu… 2 Qu…
#> 9 2 Quite we… 2 Qui… 2 Qu… 2 Qu… 3 Not … 2 Qui… 2 Qui… 2 Qui… 2 Qu… 3 No…
#> 10 2 Quite we… 3 Not… 2 Qu… 2 Qu… 3 Not … 2 Qui… 2 Qui… 4 Not… 2 Qu… 4 No…
#> # ℹ 1,290 more rows
#> # ℹ 6 more variables: DISHONB <fct>, INTELB <fct>, X.Intercept. <dbl>,
#> # PARTY <dbl>, .class <int>, .probability <dbl>
count(au, .class)
#> # A tibble: 3 × 2
#> .class n
#> <int> <int>
#> 1 1 444
#> 2 2 496
#> 3 3 360
# if the original data is provided, it leads to NAs in new columns
# for rows that weren't predicted
au2 <- augment(nes2a, data = election)
au2
#> # A tibble: 1,785 × 20
#> MORALG CARESG KNOWG LEADG DISHONG INTELG MORALB CARESB KNOWB LEADB
#> <fct> <fct> <fct> <fct> <fct> <fct> <fct> <fct> <fct> <fct>
#> 1 3 Not too … 1 Ext… 2 Qu… 2 Qu… 3 Not … 2 Qui… 1 Ext… 1 Ext… 2 Qu… 2 Qu…
#> 2 4 Not well… 3 Not… 4 No… 3 No… 2 Quit… 2 Qui… NA NA 2 Qu… 3 No…
#> 3 1 Extremel… 2 Qui… 2 Qu… 1 Ex… 3 Not … 2 Qui… 2 Qui… 2 Qui… 2 Qu… 3 No…
#> 4 2 Quite we… 2 Qui… 2 Qu… 2 Qu… 2 Quit… 2 Qui… 2 Qui… 3 Not… 2 Qu… 2 Qu…
#> 5 2 Quite we… 4 Not… 2 Qu… 3 No… 2 Quit… 2 Qui… 1 Ext… 1 Ext… 2 Qu… 2 Qu…
#> 6 2 Quite we… 3 Not… 3 No… 2 Qu… 2 Quit… 2 Qui… 2 Qui… NA 3 No… 2 Qu…
#> 7 2 Quite we… NA 2 Qu… 2 Qu… 4 Not … 2 Qui… NA 3 Not… 2 Qu… 2 Qu…
#> 8 2 Quite we… 2 Qui… 2 Qu… 2 Qu… 3 Not … 2 Qui… 3 Not… 4 Not… 4 No… 4 No…
#> 9 2 Quite we… 2 Qui… 2 Qu… 3 No… 4 Not … 2 Qui… 2 Qui… 3 Not… 2 Qu… 2 Qu…
#> 10 1 Extremel… 1 Ext… 1 Ex… 1 Ex… 4 Not … 1 Ext… 2 Qui… 4 Not… 2 Qu… 3 No…
#> # ℹ 1,775 more rows
#> # ℹ 10 more variables: DISHONB <fct>, INTELB <fct>, VOTE3 <dbl>,
#> # AGE <dbl>, EDUC <dbl>, GENDER <dbl>, PARTY <dbl>, .class <int>,
#> # .probability <dbl>, .rownames <chr>
dim(au2)
#> [1] 1785 20
相关用法
- R broom augment.polr 使用来自 (n) 个 polr 对象的信息增强数据
- R broom augment.plm 使用来自 plm 对象的信息增强数据
- R broom augment.pam 使用来自 pam 对象的信息增强数据
- R broom augment.betamfx 使用来自 betamfx 对象的信息增强数据
- R broom augment.robustbase.glmrob 使用来自 glmrob 对象的信息增强数据
- R broom augment.rlm 使用来自 rlm 对象的信息增强数据
- R broom augment.htest 使用来自(n)个 htest 对象的信息来增强数据
- R broom augment.clm 使用来自 clm 对象的信息增强数据
- R broom augment.speedlm 使用来自 speedlm 对象的信息增强数据
- R broom augment.felm 使用来自 (n) 个 felm 对象的信息来增强数据
- R broom augment.smooth.spline 整理一个(n)smooth.spline对象
- R broom augment.drc 使用来自 a(n) drc 对象的信息增强数据
- R broom augment.decomposed.ts 使用来自 decomposed.ts 对象的信息增强数据
- R broom augment.lm 使用来自 (n) lm 对象的信息增强数据
- R broom augment.rqs 使用来自 (n) 个 rqs 对象的信息来增强数据
- R broom augment.nls 使用来自 nls 对象的信息增强数据
- R broom augment.gam 使用来自 gam 对象的信息增强数据
- R broom augment.fixest 使用来自(n)个最固定对象的信息来增强数据
- R broom augment.survreg 使用来自 survreg 对象的信息增强数据
- R broom augment.rq 使用来自 a(n) rq 对象的信息增强数据
- R broom augment.Mclust 使用来自 Mclust 对象的信息增强数据
- R broom augment.nlrq 整理 a(n) nlrq 对象
- R broom augment.robustbase.lmrob 使用来自 lmrob 对象的信息增强数据
- R broom augment.lmRob 使用来自 lmRob 对象的信息增强数据
- R broom augment.mlogit 使用来自 mlogit 对象的信息增强数据
注：本文由纯净天空筛选整理自等大神的英文原创作品 Augment data with information from a(n) poLCA object。非经特殊声明，原始代码版权归原作者所有，本译文未经允许或授权，请勿转载或复制。