本文简要介绍 python 语言中 scipy.signal.ellip 的用法。
用法:
scipy.signal.ellip(N, rp, rs, Wn, btype='low', analog=False, output='ba', fs=None)#椭圆 (Cauer) 数字和模拟滤波器设计。
设计Nth-order 数字或模拟椭圆滤波器并返回滤波器系数。
- N: int
过滤器的顺序。
- rp: 浮点数
通带中允许低于单位增益的最大纹波。以分贝为单位指定,为正数。
- rs: 浮点数
阻带所需的最小衰减。以分贝为单位指定,为正数。
- Wn: array_like
给出临界频率的标量或长度为 2 的序列。对于椭圆滤波器,这是过渡带中增益首先下降到 -rp 以下的点。
对于数字滤波器,Wn 的单位与 fs 相同。默认情况下,fs 为 2 half-cycles/sample,因此这些从 0 归一化为 1,其中 1 是奈奎斯特频率。 (因此 Wn 在 half-cycles /样本中。)
对于模拟滤波器,Wn 是角频率(例如,rad/s)。
- btype: {‘lowpass’, ‘highpass’, ‘bandpass’, ‘bandstop’},可选
过滤器的类型。默认为‘lowpass’。
- analog: 布尔型,可选
如果为 True,则返回模拟滤波器,否则返回数字滤波器。
- output: {‘ba’, ‘zpk’, ‘sos’},可选
输出类型:分子/分母 (‘ba’)、pole-zero (‘zpk’) 或二阶部分 (‘sos’)。默认值为 ‘ba’ 以实现向后兼容性,但 ‘sos’ 应用于通用过滤。
- fs: 浮点数,可选
数字系统的采样频率。
- b, a: 数组,数组
分子 (b) 和分母 (a) IIR 滤波器的多项式。仅在以下情况下返回
output='ba'.- z, p, k: ndarray,ndarray,浮点数
IIR 滤波器传递函数的零点、极点和系统增益。仅在
output='zpk'时返回。- sos: ndarray
IIR 滤波器的二阶截面表示。仅在
output='sos'时返回。
参数 ::
返回 ::
注意:
椭圆滤波器也称为 Cauer 或 Zolotarev 滤波器,可最大限度地提高频率响应的通带和阻带之间的转换率,但代价是两者都出现纹波,并增加了阶跃响应中的振铃。
作为rp接近 0,椭圆滤波器变为切比雪夫 II 型滤波器 (scipy.signal.cheby2)。作为rs接近 0 时,它变成 Chebyshev I 型滤波器 (scipy.signal.cheby1)。当两者都接近 0 时,它变成了巴特沃斯滤波器 (scipy.signal.butter)。
等波纹通带有 N 个最大值或最小值(例如,5th-order 滤波器有 3 个最大值和 2 个最小值)。因此,odd-order 滤波器的 DC 增益是统一的,或者 even-order 滤波器的 DC 增益为 -rp dB。
'sos'输出参数是在 0.16.0 中添加的。例子:
设计一个模拟滤波器并绘制其频率响应,显示关键点:
>>> from scipy import signal >>> import matplotlib.pyplot as plt >>> import numpy as np>>> b, a = signal.ellip(4, 5, 40, 100, 'low', analog=True) >>> w, h = signal.freqs(b, a) >>> plt.semilogx(w, 20 * np.log10(abs(h))) >>> plt.title('Elliptic filter frequency response (rp=5, rs=40)') >>> plt.xlabel('Frequency [radians / second]') >>> plt.ylabel('Amplitude [dB]') >>> plt.margins(0, 0.1) >>> plt.grid(which='both', axis='both') >>> plt.axvline(100, color='green') # cutoff frequency >>> plt.axhline(-40, color='green') # rs >>> plt.axhline(-5, color='green') # rp >>> plt.show()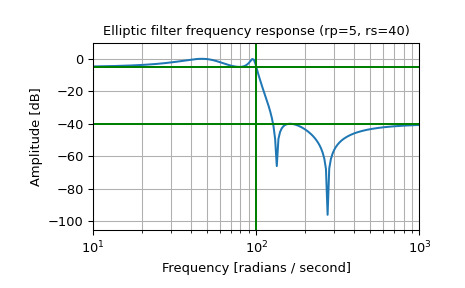
生成由 10 Hz 和 20 Hz 组成的信号,以 1 kHz 采样
>>> t = np.linspace(0, 1, 1000, False) # 1 second >>> sig = np.sin(2*np.pi*10*t) + np.sin(2*np.pi*20*t) >>> fig, (ax1, ax2) = plt.subplots(2, 1, sharex=True) >>> ax1.plot(t, sig) >>> ax1.set_title('10 Hz and 20 Hz sinusoids') >>> ax1.axis([0, 1, -2, 2])设计 17 Hz 的数字 high-pass 滤波器以消除 10 Hz 音调,并将其应用于信号。 (过滤时建议使用二阶节格式,避免传递函数(
ba)格式出现数值错误):>>> sos = signal.ellip(8, 1, 100, 17, 'hp', fs=1000, output='sos') >>> filtered = signal.sosfilt(sos, sig) >>> ax2.plot(t, filtered) >>> ax2.set_title('After 17 Hz high-pass filter') >>> ax2.axis([0, 1, -2, 2]) >>> ax2.set_xlabel('Time [seconds]') >>> plt.tight_layout() >>> plt.show()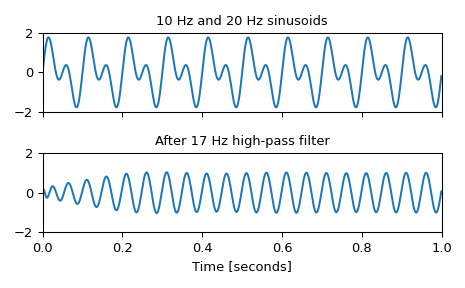
相关用法
- Python SciPy signal.ellipord用法及代码示例
- Python SciPy signal.czt_points用法及代码示例
- Python SciPy signal.chirp用法及代码示例
- Python SciPy signal.residue用法及代码示例
- Python SciPy signal.iirdesign用法及代码示例
- Python SciPy signal.max_len_seq用法及代码示例
- Python SciPy signal.kaiser_atten用法及代码示例
- Python SciPy signal.oaconvolve用法及代码示例
- Python SciPy signal.hilbert用法及代码示例
- Python SciPy signal.ricker用法及代码示例
- Python SciPy signal.group_delay用法及代码示例
- Python SciPy signal.cheb2ord用法及代码示例
- Python SciPy signal.get_window用法及代码示例
- Python SciPy signal.lfilter用法及代码示例
- Python SciPy signal.morlet用法及代码示例
- Python SciPy signal.coherence用法及代码示例
- Python SciPy signal.dfreqresp用法及代码示例
- Python SciPy signal.TransferFunction用法及代码示例
- Python SciPy signal.dbode用法及代码示例
- Python SciPy signal.residuez用法及代码示例
- Python SciPy signal.bilinear_zpk用法及代码示例
- Python SciPy signal.firls用法及代码示例
- Python SciPy signal.impulse用法及代码示例
- Python SciPy signal.buttord用法及代码示例
- Python SciPy signal.find_peaks用法及代码示例
注:本文由纯净天空筛选整理自scipy.org大神的英文原创作品 scipy.signal.ellip。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
