Python SciPy stats.tukey_hsd用法及代碼示例

本文簡要介紹 python 語言中 scipy.stats.tukey_hsd 的用法。

用法:

scipy.stats.tukey_hsd(*args)#

執行 Tukey 的 HSD 測試以確保在多個治療中均值相等。

Tukey 的誠實顯著性差異 (HSD) 檢驗對一組樣本的均值進行成對比較。 ANOVA(例如 f_oneway )評估每個樣本的真實平均值是否相同，而 Tukey 的 HSD 是一種事後檢驗，用於將每個樣本的平均值與其他樣本的平均值進行比較。

原假設是樣本的分布均具有相同的均值。針對每個可能的樣本配對計算的檢驗統計量隻是樣本均值之間的差異。對於每一對，p 值是在零假設(和其他假設；參見注釋)下觀察統計量的極值的概率，考慮到正在執行許多成對比較。還提供每對均值之間差異的置信區間。

參數 ：：

sample1, sample2, …： array_like

每組的樣本測量值。必須至少有兩個參數。

返回 ：：

result： TukeyHSDResult 實例

返回值是一個具有以下屬性的對象：

統計 浮點數數組

每次比較的測試計算統計量。索引 (i, j) 處的元素是組 i 和 j 之間比較的統計量。

p值 浮點數數組

每次比較的檢驗的計算 p 值。索引 (i, j) 處的元素是組 i 和 j 之間比較的 p 值。

該對象具有以下方法：

confidence_interval(confidence_level=0.95)：

計算指定置信水平的置信區間。

注意：

該測試的使用依賴於幾個假設。

1. 觀察在組內和組間是獨立的。

2. 每組內的觀察值呈正態分布。

3. 從中抽取樣本的分布具有相同的有限方差。

測試的原始公式是針對相同大小的樣本 [6]。在樣本量不等的情況下，測試使用Tukey-Kramer 方法 [4]。

參考：

[1]

NIST/SEMATECH e-Handbook of Statistical Methods, “7.4.7.1.圖基的方法。”https://www.itl.nist.gov/div898/handbook/prc/section4/prc471.htm, 2020 年 11 月 28 日。

[2]

Abdi、Herve & Williams、Lynne。 (2021 年)。 “Tukey 的誠實顯著差異 (HSD) 測試。”https://personal.utdallas.edu/~herve/abdi-HSD2010-pretty.pdf

[3]

“One-Way 使用 SAS PROC ANOVA 和 PROC GLM 的 ANOVA。” SAS 教程，2007 年，www.stattutorials.com/SAS/TUTORIAL-PROC-GLM.htm。

[4]

克萊默，克萊德·楊。 “將多範圍檢驗擴展到具有不相等複製數的組均值。”生物識別，第一卷。 12，沒有。 3，1956 年，第 307-310 頁。 JSTOR，www.jstor.org/stable/3001469。 2021 年 5 月 25 日訪問。

[5]

NIST/SEMATECH e-Handbook of Statistical Methods, “7.4.3.3. ANOVA 表和均值假設檢驗”https://www.itl.nist.gov/div898/handbook/prc/section4/prc433.htm, 2021 年 6 月 2 日。

[6]

Tukey, John W. “在方差分析中比較個體均值”。生物識別，第一卷。 5，沒有。 2，1949 年，第 99-114 頁。 JSTOR，www.jstor.org/stable/3001913。於 2021 年 6 月 14 日訪問。

例子：

以下是比較三種品牌的頭痛藥緩解時間的一些數據，以分鍾為單位。數據改編自[3]。

>>> import numpy as np
>>> from scipy.stats import tukey_hsd
>>> group0 = [24.5, 23.5, 26.4, 27.1, 29.9]
>>> group1 = [28.4, 34.2, 29.5, 32.2, 30.1]
>>> group2 = [26.1, 28.3, 24.3, 26.2, 27.8]

我們想看看任何組之間的方法是否有顯著差異。首先，目視檢查盒須圖。

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(1, 1)
>>> ax.boxplot([group0, group1, group2])
>>> ax.set_xticklabels(["group0", "group1", "group2"]) 
>>> ax.set_ylabel("mean") 
>>> plt.show()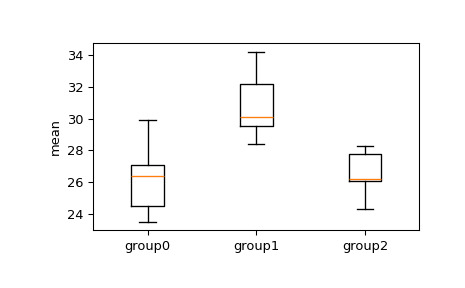

從箱線圖中，我們可以看到四分位間距組 1 到組 2 和組 3 的重疊，但我們可以應用 tukey_hsd 檢驗來確定均值之間的差異是否顯著。我們設置了 0.05 的顯著性水平來拒絕原假設。

>>> res = tukey_hsd(group0, group1, group2)
>>> print(res)
Tukey's HSD Pairwise Group Comparisons (95.0% Confidence Interval)
Comparison  Statistic  p-value   Lower CI   Upper CI
(0 - 1)     -4.600      0.014     -8.249     -0.951
(0 - 2)     -0.260      0.980     -3.909      3.389
(1 - 0)      4.600      0.014      0.951      8.249
(1 - 2)      4.340      0.020      0.691      7.989
(2 - 0)      0.260      0.980     -3.389      3.909
(2 - 1)     -4.340      0.020     -7.989     -0.691

原假設是每組均值相同。 group0 和 group1 以及 group1 和 group2 之間比較的 p 值不超過 0.05，因此我們拒絕它們具有相同均值的原假設。 group0 和 group2 之間的比較的 p 值超過 0.05，因此我們接受零假設，即它們的均值之間不存在顯著差異。

我們還可以計算與我們選擇的置信水平相關的置信區間。

>>> group0 = [24.5, 23.5, 26.4, 27.1, 29.9]
>>> group1 = [28.4, 34.2, 29.5, 32.2, 30.1]
>>> group2 = [26.1, 28.3, 24.3, 26.2, 27.8]
>>> result = tukey_hsd(group0, group1, group2)
>>> conf = res.confidence_interval(confidence_level=.99)
>>> for ((i, j), l) in np.ndenumerate(conf.low):
...     # filter out self comparisons
...     if i != j:
...         h = conf.high[i,j]
...         print(f"({i} - {j}) {l:>6.3f} {h:>6.3f}")
(0 - 1) -9.480  0.280
(0 - 2) -5.140  4.620
(1 - 0) -0.280  9.480
(1 - 2) -0.540  9.220
(2 - 0) -4.620  5.140
(2 - 1) -9.220  0.540