Python SciPy stats.goodness_of_fit用法及代碼示例

本文簡要介紹 python 語言中 scipy.stats.goodness_of_fit 的用法。

用法:

scipy.stats.goodness_of_fit(dist, data, *, known_params=None, fit_params=None, guessed_params=None, statistic='ad', n_mc_samples=9999, random_state=None)#

執行擬合優度檢驗，將數據與分布族進行比較。

給定一個分布族和數據，對數據是從該族的分布中提取的原假設進行檢驗。可以指定任何已知的分布參數。分布的其餘參數將適合數據，並相應地計算檢驗的 p 值。可以使用一些統計數據來比較分布與數據。

參數 ：：

dist： scipy.stats.rv_continuous

代表原假設下分布族的對象。

data： 一維數組

有待測試的有限的、未經審查的數據。

known_params： 字典，可選

包含 name-value 對已知分布參數的字典。蒙特卡羅樣本是使用這些參數值從 null-hypothesized 分布中隨機抽取的。在對每個蒙特卡洛樣本進行統計評估之前，僅 null-hypothesized 分布族的剩餘未知參數適合樣本；已知參數保持固定。如果分布族的所有參數已知，則省略將分布族擬合到每個樣本的步驟。

fit_params： 字典，可選

包含已適合數據的name-value 分布參數對的字典，例如使用scipy.stats.fit或者fit的方法距離。蒙特卡羅樣本是使用這些指定的參數值從 null-hypothesized 分布中抽取的。然而，在這些蒙特卡羅樣本上，null-hypothesized 分布族的這些參數和所有其他未知參數在評估統計數據之前已擬合。

guessed_params： 字典，可選

包含name-value對已被猜測的分布參數的字典。這些參數始終被視為自由參數，並且既適合所提供的數據，也適合從 null-hypothesized 分布中提取的蒙特卡洛樣本。這些guessed_params的目的是用作數值擬合過程的初始值。

statistic： {“ad”, “ks”, “cvm”, “filliben”}，可選

將分布族的未知參數擬合到數據後，用於將數據與分布進行比較的統計量。 Anderson-Darling (“ad”) [1]、Kolmogorov-Smirnov (“ks”) [1]、Cramer-von Mises (“cvm”) [1] 和 Filliben (“filliben”) [7] 統計數據為可用的。

n_mc_samples： 整數，默認值：9999

從零假設分布中抽取以形成統計零分布的蒙特卡羅樣本數。每個樣本的大小與給定數據相同。

random_state： {無，整數， numpy.random.Generator ，

numpy.random.RandomState}, optional

用於生成蒙特卡羅樣本的偽隨機數生成器狀態。

如果random_state是None(默認)，numpy.random.RandomState使用單例。如果random_state是一個 int，一個新的RandomState使用實例，播種random_state.如果random_state已經是一個Generator或者RandomState實例，然後使用提供的實例。

返回 ：：

res： GoodnessOfFitResult

具有以下屬性的對象。

fit_result FitResult

表示所提供的距離與數據的擬合度的對象。該對象包括完全定義 null-hypothesized 分布(即從中抽取蒙特卡羅樣本的分布)的分布族參數值。

統計 浮點數

將提供的數據與 null-hypothesized 分布進行比較的統計值。

p值 浮點數

零分布中統計值至少與所提供數據的統計值一樣極端的元素比例。

null_distribution ndarray

從 null-hypothesized 分布中提取的每個蒙特卡洛樣本的統計值。

注意：

這是一個廣義的蒙特卡洛 goodness-of-fit 過程，其特殊情況對應於各種 Anderson-Darling 測試、Lilliefors 測試等。該測試在 [2]、[3] 和 [4] 中說明為參數引導程序測試。這是蒙特卡羅測試，其中指定樣本分布的參數是根據數據估計的。我們自始至終都使用 “Monte Carlo” 而不是 “parametric bootstrap” 來說明測試，以避免與更熟悉的非參數引導程序混淆，並在下麵說明如何執行測試。

傳統的擬合優度檢驗

傳統上，與一組固定的顯著性水平相對應的臨界值是使用蒙特卡羅方法預先計算的。用戶通過僅計算其觀察數據的檢驗統計量值並將該值與列表中的臨界值進行比較來執行測試。這種做法不是很靈活，因為表格不適用於已知和未知參數值的所有分布和組合。此外，當從有限的表格數據中插入臨界值以與用戶的樣本大小和擬合參數值相對應時，結果可能不準確。為了克服這些缺點，該函數允許用戶執行適合其特定數據的蒙特卡羅試驗。

算法概述

簡而言之，該例程執行以下步驟：

1. Fit unknown parameters to the given data, thereby forming the “null-hypothesized” distribution, and compute the statistic of this pair of data and distribution.

2. Draw random samples from this null-hypothesized distribution.

3. Fit the unknown parameters to each random sample.

4. Calculate the statistic between each sample and the distribution that has been fit to the sample.

5. Compare the value of the statistic corresponding with data from (1) against the values of the statistic corresponding with the random samples from (4). The p-value is the proportion of samples with a statistic value greater than or equal to the statistic of the observed data.

更詳細地，步驟如下。

首先，由指定的分布族的任何未知參數距離適合所提供的數據使用最大似然估計。 (一個例外是位置和尺度未知的正態分布：我們使用偏差校正標準差np.std(data, ddof=1)對於建議的規模[1].) 這些參數值指定稱為“null-hypothesized 分布”的分布族的特定成員，即在原假設下對數據進行采樣的分布。這統計，將數據與分布進行比較，計算結果為數據和null-hypothesized分布。

接下來，從 null-hypothesized 分布中抽取許多(具體為 n_mc_samples)新樣本，每個樣本包含與數據相同數量的觀察值。分布族 dist 的所有未知參數都適合每個重采樣，並且在每個樣本與其相應的擬合分布之間計算統計量。這些統計值形成了蒙特卡洛零分布(不要與上麵的“null-hypothesized 分布”混淆)。

檢驗的 p 值是蒙特卡羅零分布中至少與所提供數據的統計值一樣極端的統計值的比例。更準確地說，p 值由下式給出

\[p = \frac{b + 1} {m + 1}\]

其中\(b\)是蒙特卡羅零分布中大於或等於計算的統計值的統計值的數量數據， 和\(m\)是蒙特卡羅零分布中的元素數量 (n_mc_samples)。添加的\(1\)分子和分母可以被認為包括與數據在零分布中，但更正式的解釋在[5].

限製

對於某些分布族，測試可能非常慢，因為分布族的未知參數必須適合每個蒙特卡羅樣本，並且對於 SciPy 中的大多數分布，通過數值優化執行分布擬合。

反模式

因此，將(由用戶)預先擬合數據的分布參數視為 known_params 可能很誘人，因為分布的所有參數的規範排除了將分布擬合到每個 Monte 的需要。卡洛樣本。 (這本質上就是原始 Kilmogorov-Smirnov 檢驗的執行方式。)盡管這樣的檢驗可以提供反對零假設的證據，但該檢驗是保守的，因為較小的 p 值往往會(大大)高估使I 類錯誤(即，盡管原假設為真，但仍拒絕原假設)，並且檢驗的功效較低(即，即使原假設為假，也不太可能拒絕原假設)。這是因為蒙特卡羅樣本不太可能與 null-hypothesized 分布以及數據一致。這往往會增加零分布中記錄的統計值，從而使更多的統計值超過數據的統計值，從而誇大 p 值。

參考：

[1] (1,2,3,4,5)

M.A.斯蒂芬斯(1974)。 “EDF 擬合優度統計數據和一些比較。”美國統計協會雜誌，卷。 69，第 730-737 頁。

[2]

W. Stute、W. G. Manteiga 和 M. P. Quindimil (1993)。 “基於引導goodness-of-fit-tests。”梅特裏卡 40.1：243-256。

[3]

C. Genest 和 B Rémillard。 (2008)。 “半參數模型中 goodness-of-fit 測試的參數引導程序的有效性。” 《IHP 概率與統計年鑒》。卷。 44.第6號。

[4]

I.Kojadinovic 和 J.Yan (2012)。 “Goodness-of-fit 基於加權引導程序的測試：參數引導程序的快速 large-sample 替代方案。”加拿大統計雜誌 40.3：480-500。

[5]

B. Phipson 和 G. K. Smyth (2010)。 “排列 P 值不應該為零：隨機抽取排列時計算精確的 P 值。” 9.1 遺傳學和分子生物學中的統計應用

[6]

H.W.利利福斯 (1967)。 “關於均值和方差未知的 Kolmogorov-Smirnov 正態性檢驗。”美國統計協會雜誌 62.318：399-402。

[7]

Filliben，James J.“正態性的概率圖相關係數檢驗。”技術計量學 17.1 (1975)：111-117。

例子：

數據從給定分布中抽取的原假設的一個眾所周知的檢驗是 Kolmogorov-Smirnov (KS) 檢驗，在 SciPy 中以 scipy.stats.ks_1samp 形式提供。假設我們希望測試以下數據是否：

>>> import numpy as np
>>> from scipy import stats
>>> rng = np.random.default_rng()
>>> x = stats.uniform.rvs(size=75, random_state=rng)

從正態分布中抽樣。為了執行 KS 檢驗，觀測數據的經驗分布函數將與正態分布的(理論)累積分布函數進行比較。當然，為此，必須完全指定原假設下的正態分布。這通常是通過首先將分布的 loc 和 scale 參數擬合到觀察到的數據，然後執行測試來完成的。

>>> loc, scale = np.mean(x), np.std(x, ddof=1)
>>> cdf = stats.norm(loc, scale).cdf
>>> stats.ks_1samp(x, cdf)
KstestResult(statistic=0.1119257570456813, pvalue=0.2827756409939257)

KS-test 的優點是可以準確、高效地計算 p 值(在零假設下獲得與從觀測數據獲得的值一樣極端的檢驗統計量值的概率)。 goodness_of_fit 隻能近似這些結果。

>>> known_params = {'loc': loc, 'scale': scale}
>>> res = stats.goodness_of_fit(stats.norm, x, known_params=known_params,
...                             statistic='ks', random_state=rng)
>>> res.statistic, res.pvalue
(0.1119257570456813, 0.2788)

統計數據完全匹配，但 p 值是通過形成“蒙特卡洛零分布”來估計的，即通過使用提供的參數從 scipy.stats.norm 中顯式抽取隨機樣本並計算每個樣本的統計量。這些統計值的分數至少與 res.statistic 一樣極端，近似於 scipy.stats.ks_1samp 計算的精確 p 值。

然而，在許多情況下，我們更願意隻測試數據是從以下之一采樣的：任何正態分布家族的成員，不是專門來自位置和尺度適合觀察樣本的正態分布。在這種情況下，利利福斯[6]認為 KS 檢驗過於保守(即 p 值高估了拒絕真實原假設的實際概率)，因此缺乏功效——當原假設實際上為假時拒絕原假設的能力。事實上，我們上麵的 p 值約為 0.28，這個值太大，無法在任何常見的顯著性水平上拒絕原假設。

考慮一下為什麽會這樣。請注意，在上麵的 KS 檢驗中，統計量始終將數據與擬合到的正態分布的 CDF 進行比較觀測數據。這往往會降低觀測數據的統計值，但在計算其他樣本的統計值時，例如我們隨機抽取形成蒙特卡羅零分布的樣本，它就是“unfair”。糾正這一點很容易：每當我們計算樣本的 KS 統計量時，我們都會使用擬合的正態分布的 CDF那個樣本。這種情況下的零分布尚未被精確計算，並且通常使用如上所述的蒙特卡羅方法來近似。這是哪裏goodness_of_fit表現出色。

>>> res = stats.goodness_of_fit(stats.norm, x, statistic='ks',
...                             random_state=rng)
>>> res.statistic, res.pvalue
(0.1119257570456813, 0.0196)

事實上，這個 p 值要小得多，並且小到足以(正確地)拒絕常見顯著性水平(包括 5% 和 2.5%)的原假設。

然而，KS 統計量對所有偏離正態性的情況都不是很敏感。 KS 統計量的最初優點是能夠從理論上計算零分布，但現在可以使用更敏感的統計量(導致更高的測試功效)，因為我們可以通過計算來近似零分布。 Anderson-Darling 統計量 [1] 往往更加敏感，並且已使用蒙特卡羅方法針對各種顯著性水平和樣本量對該統計量的臨界值進行了製表。

>>> res = stats.anderson(x, 'norm')
>>> print(res.statistic)
1.2139573337497467
>>> print(res.critical_values)
[0.549 0.625 0.75  0.875 1.041]
>>> print(res.significance_level)
[15.  10.   5.   2.5  1. ]

這裏，統計量的觀察值超過了對應於1%顯著性水平的臨界值。這告訴我們觀測數據的 p 值小於 1%，但它是什麽呢？我們可以根據這些 (already-interpolated) 值進行插值，但 goodness_of_fit 可以直接估計它。

>>> res = stats.goodness_of_fit(stats.norm, x, statistic='ad',
...                             random_state=rng)
>>> res.statistic, res.pvalue
(1.2139573337497467, 0.0034)

另一個優點是，goodness_of_fit 的使用不限於參數已知與必須根據數據估計的一組特定分布或條件。相反，goodness_of_fit 可以使用足夠快速且可靠的 fit 方法相對快速地估計任何分布的 p 值。例如，在這裏，我們使用 Cramer-von Mises 統計量針對已知位置和未知尺度的瑞利分布執行擬合優度檢驗。

>>> rng = np.random.default_rng()
>>> x = stats.chi(df=2.2, loc=0, scale=2).rvs(size=1000, random_state=rng)
>>> res = stats.goodness_of_fit(stats.rayleigh, x, statistic='cvm',
...                             known_params={'loc': 0}, random_state=rng)

執行速度相當快，但為了檢查 fit 方法的可靠性，我們應該檢查擬合結果。

>>> res.fit_result  # location is as specified, and scale is reasonable
  params: FitParams(loc=0.0, scale=2.1026719844231243)
 success: True
 message: 'The fit was performed successfully.'
>>> import matplotlib.pyplot as plt  # matplotlib must be installed to plot
>>> res.fit_result.plot()
>>> plt.show()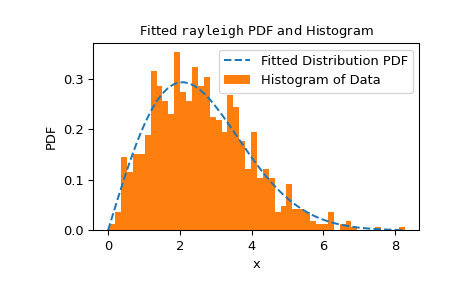

如果分布不太適合觀察到的數據，則檢驗可能無法控製 I 類錯誤率，即拒絕原假設(即使原假設為真)的機會。

我們還應該尋找零分布中可能由不可靠擬合引起的極端異常值。這些並不一定會使結果無效，但它們往往會降低測試的功效。

>>> _, ax = plt.subplots()
>>> ax.hist(np.log10(res.null_distribution))
>>> ax.set_xlabel("log10 of CVM statistic under the null hypothesis")
>>> ax.set_ylabel("Frequency")
>>> ax.set_title("Histogram of the Monte Carlo null distribution")
>>> plt.show()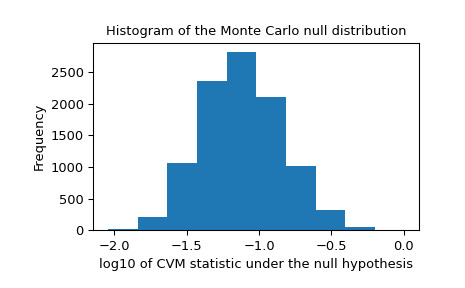

這個劇情看起來讓人安心。

如果 fit 方法工作可靠，並且檢驗統計量的分布對擬合參數的值不是特別敏感，則 goodness_of_fit 提供的 p 值預計將是一個很好的近似值。

>>> res.statistic, res.pvalue
(0.2231991510248692, 0.0525)