本文簡要介紹 python 語言中 scipy.stats.geninvgauss 的用法。
用法:
scipy.stats.geninvgauss = <scipy.stats._continuous_distns.geninvgauss_gen object>#廣義逆高斯連續隨機變量。
作為
rv_continuous類的實例,geninvgauss對象從它繼承了一組通用方法(完整列表見下文),並用特定於此特定發行版的詳細信息來完成它們。注意:
geninvgauss的概率密度函數為:其中x > 0,p是一個實數並且b > 0([1])。是二階修正貝塞爾函數p(scipy.special.kv)。
上麵的概率密度在“standardized” 表格中定義。要移動和/或縮放分布,請使用
loc和scale參數。具體來說,geninvgauss.pdf(x, p, b, loc, scale)等同於geninvgauss.pdf(y, p, b) / scale和y = (x - loc) / scale。請注意,移動分布的位置不會使其成為“noncentral” 分布;某些分布的非中心概括可在單獨的類中獲得。逆高斯分布stats.invgauss(mu)是一個特例
geninvgauss和p = -1/2,b = 1 /mu和規模 = 畝.對於這種分布,生成隨機變量具有挑戰性。該實現基於[2]。
參考:
[1]O.Barndorff-Nielsen、P. Blaesild、C. Halgreen,“廣義逆高斯分布的首次命中時間模型”,隨機過程及其應用,第 7 期,第 49-54 頁,1978 年。
[2]W. Hoermann 和 J. Leydold,“生成廣義逆高斯隨機變量”,統計與計算,24(4),p。 547-557,2014 年。
例子:
>>> import numpy as np >>> from scipy.stats import geninvgauss >>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots(1, 1)計算前四個時刻:
>>> p, b = 2.3, 1.5 >>> mean, var, skew, kurt = geninvgauss.stats(p, b, moments='mvsk')顯示概率密度函數(
pdf):>>> x = np.linspace(geninvgauss.ppf(0.01, p, b), ... geninvgauss.ppf(0.99, p, b), 100) >>> ax.plot(x, geninvgauss.pdf(x, p, b), ... 'r-', lw=5, alpha=0.6, label='geninvgauss pdf')或者,可以調用分布對象(作為函數)來固定形狀、位置和比例參數。這將返回一個 “frozen” RV 對象,其中包含固定的給定參數。
凍結分布並顯示凍結的
pdf:>>> rv = geninvgauss(p, b) >>> ax.plot(x, rv.pdf(x), 'k-', lw=2, label='frozen pdf')檢查
cdf和ppf的準確性:>>> vals = geninvgauss.ppf([0.001, 0.5, 0.999], p, b) >>> np.allclose([0.001, 0.5, 0.999], geninvgauss.cdf(vals, p, b)) True生成隨機數:
>>> r = geninvgauss.rvs(p, b, size=1000)並比較直方圖:
>>> ax.hist(r, density=True, bins='auto', histtype='stepfilled', alpha=0.2) >>> ax.set_xlim([x[0], x[-1]]) >>> ax.legend(loc='best', frameon=False) >>> plt.show()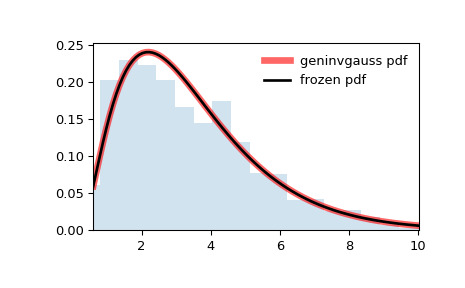
相關用法
- Python SciPy stats.genpareto用法及代碼示例
- Python SciPy stats.genlogistic用法及代碼示例
- Python SciPy stats.gennorm用法及代碼示例
- Python SciPy stats.genhalflogistic用法及代碼示例
- Python SciPy stats.genexpon用法及代碼示例
- Python SciPy stats.genhyperbolic用法及代碼示例
- Python SciPy stats.gengamma用法及代碼示例
- Python SciPy stats.genextreme用法及代碼示例
- Python SciPy stats.geom用法及代碼示例
- Python SciPy stats.gumbel_l用法及代碼示例
- Python SciPy stats.gzscore用法及代碼示例
- Python SciPy stats.gompertz用法及代碼示例
- Python SciPy stats.gibrat用法及代碼示例
- Python SciPy stats.gmean用法及代碼示例
- Python SciPy stats.gamma用法及代碼示例
- Python scipy.stats.gilbrat用法及代碼示例
- Python SciPy stats.gstd用法及代碼示例
- Python SciPy stats.gaussian_kde用法及代碼示例
- Python SciPy stats.gumbel_r用法及代碼示例
- Python SciPy stats.gausshyper用法及代碼示例
- Python SciPy stats.goodness_of_fit用法及代碼示例
- Python SciPy stats.anderson用法及代碼示例
- Python SciPy stats.iqr用法及代碼示例
- Python SciPy stats.skewnorm用法及代碼示例
- Python SciPy stats.cosine用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.stats.geninvgauss。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
