Python SciPy stats.gaussian_kde用法及代碼示例

本文簡要介紹 python 語言中 scipy.stats.gaussian_kde 的用法。

用法:

class  scipy.stats.gaussian_kde(dataset, bw_method=None, weights=None)#

使用高斯核表示 kernel-density 估計。

核密度估計是一種以非參數方式估計隨機變量的概率密度函數(PDF)的方法。 gaussian_kde 適用於 uni-variate 和 multi-variate 數據。它包括自動帶寬確定。該估計最適合單峰分布；雙峰或 multi-modal 分布往往會過度平滑。

參數 ：：

dataset： array_like

要估計的數據點。在單變量數據的情況下，這是一個一維數組，否則是一個具有形狀(# of dims，# of data)的二維數組。

bw_method： str，標量或可調用，可選

用於計算估計器帶寬的方法。這可以是‘scott’, ‘silverman’、標量常量或可調用對象。如果是標量，這將直接用作kde.factor.如果是可調用的，它應該需要一個gaussian_kde實例作為唯一參數並返回一個標量。如果無(默認)，則使用‘scott’。有關詳細信息，請參閱注釋。

weights： 數組，可選

數據點的權重。這必須與數據集的形狀相同。如果 None (默認)，則假定樣本的權重相同

注意：

帶寬選擇強烈影響從 KDE 獲得的估計(比內核的實際形狀影響更大)。帶寬選擇可以通過“rule of thumb”、交叉驗證、“插件方法”或其他方式來完成；評論見[3]、[4]。 gaussian_kde 使用經驗法則，默認為斯科特規則。

斯科特規則 [1]，實現為 scotts_factor ，是：

n**(-1./(d+4)),

n 是數據點的數量，d 是維度的數量。在權重不相等的點的情況下， scotts_factor 變為：

neff**(-1./(d+4)),

neff 為有效數據點數量。西爾弗曼規則 [2]，實現為 silverman_factor ，是：

(n * (d + 2) / 4.)**(-1. / (d + 4)).

或者在權重不相等的情況下：

(neff * (d + 2) / 4.)**(-1. / (d + 4)).

核密度估計的一般說明可以在 [1] 和 [2] 中找到，這種多維實現的數學可以在 [1] 中找到。

使用一組加權樣本，數據點neff 的有效數量由下式定義：

neff = sum(weights)^2 / sum(weights^2)

詳見[5]。

gaussian_kde 當前不支持位於其表達空間的 lower-dimensional 子空間中的數據。對於此類數據，請考慮執行主成分分析/降維並對轉換後的數據使用gaussian_kde。

參考：

[1] (1,2,3)

D.W. Scott，“多元密度估計：理論、實踐和可視化”，John Wiley & Sons，紐約，奇斯特，1992 年。

[2] (1,2)

BW西爾弗曼，“統計和數據分析的密度估計”，卷。 26，統計和應用概率專著，查普曼和霍爾，倫敦，1986 年。

[3]

學士學位Turlach，“核密度估計中的帶寬選擇：回顧”，CORE 和 Institut de Statistique，Vol。 19，第 1-33 頁，1993 年。

[4]

D.M.巴什坦尼克和 R.J. Hyndman，“核條件密度估計的帶寬選擇”，計算統計與數據分析，卷。 36，第 279-298 頁，2001 年。

[5]

Gray P.G.，1969 年，皇家統計學會雜誌。係列 A(一般)、132、272

例子：

生成一些隨機的二維數據：

>>> import numpy as np
>>> from scipy import stats
>>> def measure(n):
...     "Measurement model, return two coupled measurements."
...     m1 = np.random.normal(size=n)
...     m2 = np.random.normal(scale=0.5, size=n)
...     return m1+m2, m1-m2

>>> m1, m2 = measure(2000)
>>> xmin = m1.min()
>>> xmax = m1.max()
>>> ymin = m2.min()
>>> ymax = m2.max()

對數據執行核密度估計：

>>> X, Y = np.mgrid[xmin:xmax:100j, ymin:ymax:100j]
>>> positions = np.vstack([X.ravel(), Y.ravel()])
>>> values = np.vstack([m1, m2])
>>> kernel = stats.gaussian_kde(values)
>>> Z = np.reshape(kernel(positions).T, X.shape)

繪製結果：

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> ax.imshow(np.rot90(Z), cmap=plt.cm.gist_earth_r,
...           extent=[xmin, xmax, ymin, ymax])
>>> ax.plot(m1, m2, 'k.', markersize=2)
>>> ax.set_xlim([xmin, xmax])
>>> ax.set_ylim([ymin, ymax])
>>> plt.show()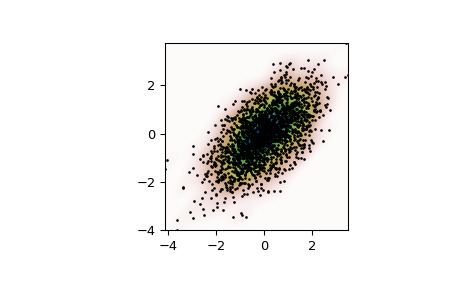

屬性 ：：

dataset： ndarray

用於初始化 gaussian_kde 的數據集。

d： int

維數。

n： int

數據點的數量。

neff： int

有效數據點數。

factor： 浮點數

帶寬因子，從 kde.covariance_factor 獲得。 kde.factor的平方乘以kde估計中數據的協方差矩陣。

covariance： ndarray

數據集的協方差矩陣，按計算的帶寬 (kde.factor) 縮放。

inv_cov： ndarray

協方差的倒數。