Python SciPy stats.fit用法及代碼示例

本文簡要介紹 python 語言中 scipy.stats.fit 的用法。

用法:

scipy.stats.fit(dist, data, bounds=None, *, guess=None, method='mle', optimizer=<function differential_evolution>)#

將離散或連續分布擬合到數據

給定分布、數據和分布參數的界限，返回參數的最大似然估計。

參數 ：：

dist： scipy.stats.rv_continuous 或 scipy.stats.rv_discrete

表示要適合數據的分布的對象。

data： 一維數組

要擬合分布的數據。如果數據包含 np.nan 、 np.inf 或 - np.inf 中的任何一個，則 fit 方法將引發 ValueError 。

bounds： 字典或元組序列，可選

如果是字典，則每個鍵是分布參數的名稱，對應的值是包含該參數下限和上限的元組。如果僅針對該參數的有限值範圍定義分布，則不需要該參數的條目；例如，某些分布的參數必須在區間 [0, 1] 上。參數位置(loc)和比例(scale)的界限是可選的；默認情況下，它們分別固定為 0 和 1。

如果是一個序列，元素 i 是一個元組，包含分布的第 i 個參數的下限和上限。在這種情況下，必須提供所有分布形狀參數的界限。可選地，位置和規模的界限可以遵循分布形狀參數。

如果形狀要保持固定(例如，如果它是已知的)，則下限和上限可能相等。如果用戶提供的下限或上限超出了定義分布的域的邊界，則分布域的邊界將替換用戶提供的值。同樣，必須為整數的參數將被限製為用戶提供的範圍內的整數值。

guess： dict 或 數組，可選

如果是字典，每個key是分布的一個參數的名字，對應的value是對參數值的猜測。

如果是一個序列，元素 i 是分布的第 i 個參數的猜測。在這種情況下，必須提供對所有分布形狀參數的猜測。

如果未提供猜測，則決策變量的猜測將不會傳遞給優化器。如果提供了guess，則任何缺失參數的猜測值將設置為下限和上限的平均值。必須為整數的參數的猜測將被四舍五入為整數值，並且位於用戶提供的邊界和分布域的交集之外的猜測將被剪裁。

method： {‘mle’, ‘mse’}

使用method="mle"(默認)，通過最小化負對數似然函數來計算擬合。對於超出分布支持的觀測值，應用較大的有限懲罰(而不是無限負對數似然)。對於 method="mse" ，通過最小化負 log-product 間距函數來計算擬合。對於超出支持範圍的觀察結果也適用同樣的懲罰。我們遵循[1]的方法，該方法適用於重複觀察的樣本。

optimizer： 可調用的，可選的

優化器是一個可調用的，它接受以下位置參數。

樂趣 可調用的

要優化的目標函數。樂趣接受一個論點x，分布的候選形狀參數，並返回給定的目標函數值x,距離，以及提供的數據.的工作優化器是找到最小化的決策變量的值樂趣.

優化器還必須接受以下關鍵字參數。

界限 元組序列

決策變量值的界限；每個元素都是一個元組，包含決策變量的下限和上限。

如果提供了guess，優化器還必須接受以下關鍵字參數。

x0 array_like

每個決策變量的猜測。

如果分布具有任何必須是整數的形狀參數，或者分布是離散的且位置參數不固定，則優化器還必須接受以下關鍵字參數。

完整性 數組 布爾值

對於每個決策變量，如果決策變量必須限製為整數值，則為 True；如果決策變量是連續的，則為 False。

優化器必須返回一個對象，例如scipy.optimize.OptimizeResult，它保存屬性中決策變量的最優值x.如果屬性fun,status， 或者message提供，它們將包含在返回的結果對象中fit.

返回 ：：

result： FitResult

具有以下字段的對象。

參數 命名元組

包含分布的形狀參數、位置和(如果適用)尺度的最大似然估計值的命名元組。

成功 布爾或無

優化器是否認為優化成功終止。

信息 str 或 None

優化器提供的任何狀態消息。

該對象具有以下方法：

nllf(參數=無，數據=無)

默認情況下，給定數據的擬合參數處的負log-likehood 函數。接受包含可選形狀、位置和分布比例以及可選數據數組的元組。

情節(軸=無)

將擬合分布的 PDF/PMF 疊加在數據的歸一化直方圖上。

注意：

當用戶提供包含最大似然估計的嚴格界限時，優化更有可能收斂到最大似然估計。例如，當對數據進行二項分布擬合時，每個樣本的實驗次數可能是已知的，在這種情況下，可以固定相應的形狀參數n。

參考：

[1]

邵永照和馬喬裏·哈恩 (Marjorie G. Hahn)。 “間距法的最大乘積：具有強一致性說明的統一公式。”伊利諾伊州數學雜誌 43.3 (1999): 489-499。

例子：

假設我們希望將分布擬合到以下數據。

>>> import numpy as np
>>> from scipy import stats
>>> rng = np.random.default_rng()
>>> dist = stats.nbinom
>>> shapes = (5, 0.5)
>>> data = dist.rvs(*shapes, size=1000, random_state=rng)

假設我們不知道數據是如何生成的，但我們懷疑它遵循帶參數的負二項分布n和p. (看scipy.stats.nbinom.) 我們認為參數n小於 30，我們知道參數p必須位於區間 [0, 1] 上。我們將這些信息記錄在一個變量中界限並將此信息傳遞給fit.

>>> bounds = [(0, 30), (0, 1)]
>>> res = stats.fit(dist, data, bounds)

fit在用戶指定的範圍內搜索界限對於與數據最匹配的值(在最大似然估計的意義上)。在這種情況下，它發現了與實際生成數據的形狀值相似的形狀值。

>>> res.params
FitParams(n=5.0, p=0.5028157644634368, loc=0.0)  # may vary

我們可以通過將分布的概率質量函數(形狀適合數據)疊加到數據的歸一化直方圖上來可視化結果。

>>> import matplotlib.pyplot as plt  # matplotlib must be installed to plot
>>> res.plot()
>>> plt.show()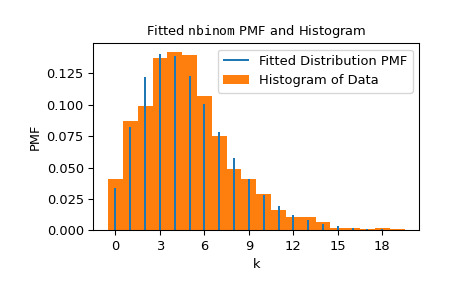

請注意，估計為n完全是整數；這是因為scipy.stats.nbinomPMF 僅包括積分n, 和scipy.stats.nbinom對象“knows”。scipy.stats.nbinom也知道形狀p必須是介於 0 和 1 之間的值。在這種情況下 - 當分布的域相對於參數是有限的時 - 我們不需要指定參數的界限。

>>> bounds = {'n': (0, 30)}  # omit parameter p using a `dict`
>>> res2 = stats.fit(dist, data, bounds)
>>> res2.params
FitParams(n=5.0, p=0.5016492009232932, loc=0.0)  # may vary

如果我們希望強製分布擬合 n 固定為 6，我們可以將 n 的下限和上限都設置為 6。但是請注意，被優化的目標函數的值通常更差(更高)這個案例。

>>> bounds = {'n': (6, 6)}  # fix parameter `n`
>>> res3 = stats.fit(dist, data, bounds)
>>> res3.params
FitParams(n=6.0, p=0.5486556076755706, loc=0.0)  # may vary
>>> res3.nllf() > res.nllf()
True  # may vary

請注意，前麵示例的數值結果是典型的，但它們可能會有所不同，因為fit,scipy.optimize.differential_evolution, 是隨機的。但是，我們可以自定義優化器使用的設置以確保可重複性 - 甚至完全使用不同的優化器 - 使用優化器範圍。

>>> from scipy.optimize import differential_evolution
>>> rng = np.random.default_rng()
>>> def optimizer(fun, bounds, *, integrality):
...     return differential_evolution(fun, bounds, strategy='best2bin',
...                                   seed=rng, integrality=integrality)
>>> bounds = [(0, 30), (0, 1)]
>>> res4 = stats.fit(dist, data, bounds, optimizer=optimizer)
>>> res4.params
FitParams(n=5.0, p=0.5015183149259951, loc=0.0)